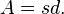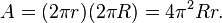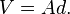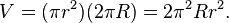Pappus's centroid theorem

In mathematics, Pappus' centroid theorem (also known as the Guldinus theorem, Pappus–Guldinus theorem or Pappus' theorem) is either of two related theorems dealing with the surface areas and volumes of surfaces and solids of revolution.
The theorem is attributed to Pappus of Alexandria and Paul Guldin.
The first theorem
The first theorem states that the surface area A of a surface of revolution generated by rotating a plane curve C about an axis external to C and on the same plane is equal to the product of the arc length s of C and the distance d traveled by its geometric centroid.
For example, the surface area of the torus with minor radius r and major radius R is
The second theorem
The second theorem states that the volume V of a solid of revolution generated by rotating a plane figure F about an external axis is equal to the product of the area A of F and the distance d traveled by its geometric centroid.
For example, the volume of the torus with minor radius r and major radius R is
Generalizations
The theorem can be generalized for arbitrary curves and shapes, under appropriate conditions.[1]
References
- ↑ Goodman, A. W.; Goodman, G. "Generalizations of the Theorems of Pappus". JSTOR. The American Mathematical Monthly. Retrieved 2014-06-28.