Palatini variation

In general relativity and gravitation the Palatini variation is nowadays thought of as variation of a Lagrangian with respect to the connection. In fact, as is well known, the Einstein-Hilbert action for general relativity was first formulated purely in terms of the spacetime metric 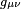\scriptstyle {g_{\mu\nu}}. In the Palatini variational method one takes as independent field variables not only the ten components 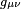\scriptstyle {g_{\mu\nu}} but also the forty components of the affine connection 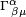\scriptstyle {\Gamma^{\alpha}_{\,\beta\mu}}, assuming, a priori, no dependence of the 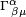\scriptstyle {\Gamma^{\alpha}_{\,\beta\mu}} from the 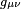\scriptstyle {g_{\mu\nu}} and their derivatives.

The reason that Palatini variation is considered important is that it means that the use of the Christoffel connection in general relativity does not have to be added as a separate assumption, the information is already in the Lagrangian. For theories of gravitation which have more complex lagrangians than the Einstein-Hilbert Lagrangian of general relativity Palatini variation sometimes gives more complex connections and sometimes tensorial equations.

Attilio Palatini (1889-1949) was an Italian mathematician who received his doctorate from the University of Padova, where he studied under Levi-Civita and Ricci-Curbastro.

The history of the subject, and Palatini's connection with it, is not straightfoward, see the references. In fact, it seems that what the textbooks now call Palatini formalism was actually invented in 1925 by Einstein and as the years passed people tended to mix up the Palatini identity and the Palatini formalism.

See also

References