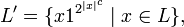Padding argument
In computational complexity theory, the padding argument is a tool to conditionally prove that if some complexity classes are equal, then some other bigger classes are also equal.
Example
The proof that P = NP implies EXP = NEXP uses "padding". 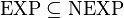 by definition, so it suffices to show
by definition, so it suffices to show 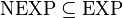 .
.
Let L be a language in NEXP. Since L is in NEXP, there is a non-deterministic Turing machine M that decides L in time 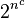 for some constant c. Let
for some constant c. Let
where 1 is a symbol not occurring in L. First we show that 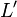 is in NP, then we will use the deterministic polynomial time machine given by P = NP to show that L is in EXP.
is in NP, then we will use the deterministic polynomial time machine given by P = NP to show that L is in EXP.
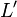 can be decided in non-deterministic polynomial time as follows. Given input
can be decided in non-deterministic polynomial time as follows. Given input 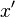 , verify that it has the form
, verify that it has the form 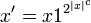 and reject if it does not. If it has the correct form, simulate M(x). The simulation takes non-deterministic
and reject if it does not. If it has the correct form, simulate M(x). The simulation takes non-deterministic 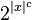 time, which is polynomial in the size of the input,
time, which is polynomial in the size of the input, 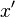 . So,
. So, 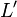 is in NP. By the assumption P = NP, there is also a deterministic machine DM that decides
is in NP. By the assumption P = NP, there is also a deterministic machine DM that decides 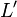 in polynomial time. We can then decide L in deterministic exponential time as follows. Given input
in polynomial time. We can then decide L in deterministic exponential time as follows. Given input  , simulate
, simulate 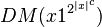 . This takes only exponential time in the size of the input,
. This takes only exponential time in the size of the input,  .
.
The 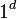 is called the "padding" of the language L. This type of argument is also sometimes used for space complexity classes, alternating classes, and bounded alternating classes.
is called the "padding" of the language L. This type of argument is also sometimes used for space complexity classes, alternating classes, and bounded alternating classes.
References
- Arora, Sanjeev; Barak, Boaz (2009), Computational Complexity: A Modern Approach, Cambridge, p. 57, ISBN 978-0-521-42426-4