PRO (category theory)

In category theory, a PRO is a strict monoidal category whose objects are the natural numbers (including zero), and whose tensor product is given on objects by the addition on numbers.

Some examples of PROs:

• the discrete category 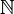of natural numbers,
• the category FinSet of natural numbers and functions between them,
• the category Bij of natural numbers and bijections,
• the category Bij_Braid of natural numbers, equipped with the braid group B_n as the automorphisms of each n (and no other morphisms).
• the category Inj of natural numbers and injections,
• the simplex category 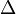of natural numbers and monotonic functions.

The name PRO is an abbreviation of "PROduct category". PROBs and PROPs are defined similarly with the additional requirement for the category to be braided, and to have a symmetry (that is, a permutation), respectively. All of the examples above are PROPs, except for the simplex category and Bij_Braid; the latter is a PROB but not a PROP, and the former is not even a PROB.

Algebras of a PRO

An algebra of a PRO in a monoidal category is a strict monoidal functor from to . Every PRO and category give rise to a category 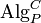of algebras whose objects are the algebras of in and whose morphisms are the natural transformations between them.

For example:

• an algebra of 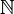is just an object of ,
• an algebra of FinSet is a commutative monoid object of ,
• an algebra of 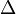is a monoid object in .

More precisely, what we mean here by "the algebras of 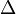in are the monoid objects in " for example is that the category of algebras of in is equivalent to the category of monoids in .

See also

• Lawvere theory

References

• Saunders MacLane (1965). "Categorical Algebra". Bulletin of the American Mathematical Society 71: 40–106. doi:10.1090/S0002-9904-1965-11234-4. 

• Tom Leinster (2004). Higher Operads, Higher Categories. Cambridge University Press.