p-stable group

Not to be confused with Stable group.

In finite group theory, a p-stable group for an odd prime p is a finite group satisfying a technical condition introduced by Gorenstein and Walter (1964, p.169, 1965) in order to extend Thompson's uniqueness results in the odd order theorem to groups with dihedral Sylow 2-subgroups.

Definitions

There are several equivalent definitions of a p-stable group.

First definition.

We give definition of a p-stable group in two parts. The definition used here comes from (Glauberman 1968, p. 1104).

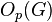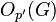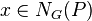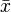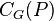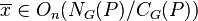1. Let p be an odd prime and G be a finite group with a nontrivial p-core O_p(G). Then G is p-stable if it satisfies the following condition: Let P be an arbitrary p-subgroup of G such that O_{p^\prime}(G) is a normal subgroup of G. Suppose that x\in N_G(P) and \bar x is the coset of C_G(P) containing x. If [P,x,x]=1, then \overline{x}\in O_n(N_G(P)/C_G(P)).

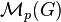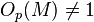Now, define \mathcal{M}_p(G) as the set of all p-subgroups of G maximal with respect to the property that O_p(M)\not= 1.

2. Let G be a finite group and p an odd prime. Then G is called p-stable if every element of 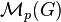\mathcal{M}_p(G) is p-stable by definition 1.

Second definition.

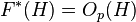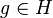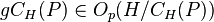Let p be an odd prime and H a finite group. Then H is p-stable if F^*(H)=O_p(H) and, whenever P is a normal p-subgroup of H and g \in H with [P,g,g]=1, then gC_H(P)\in O_p(H/C_H(P)).

Properties

If p is an odd prime and G is a finite group such that SL2(p) is not involved in G, then G is p-stable. If furthermore G contains a normal p-subgroup P such that 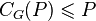C_G(P)\leqslant P, then 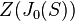Z(J_0(S)) is a characteristic subgroup of G, where 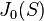J_0(S) is the subgroup introduced by John Thompson in (Thompson 1969, pp. 149–151).

See also

References