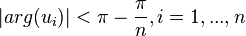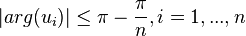P-matrix
In mathematics, a  -matrix is a complex square matrix with every principal minor > 0. A closely related class is that of
-matrix is a complex square matrix with every principal minor > 0. A closely related class is that of  -matrices, which are the closure of the class of
-matrices, which are the closure of the class of  -matrices, with every principal minor
-matrices, with every principal minor  0.
0.
Spectra of  -matrices
-matrices
By a theorem of Kellogg, the eigenvalues of  - and
- and 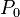 - matrices are bounded away from a wedge about the negative real axis as follows:
- matrices are bounded away from a wedge about the negative real axis as follows:
- If
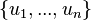 are the eigenvalues of an
are the eigenvalues of an  -dimensional
-dimensional  -matrix, then
-matrix, then
- If
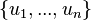 ,
, 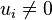 ,
, 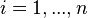 are the eigenvalues of an
are the eigenvalues of an  -dimensional
-dimensional 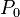 -matrix, then
-matrix, then
Remarks
The class of nonsingular M-matrices is a subset of the class of  -matrices. More precisely, all matrices that are both
-matrices. More precisely, all matrices that are both  -matrices and Z-matrices are nonsingular
-matrices and Z-matrices are nonsingular 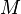 -matrices. The class of sufficient matrices is another generalization of
-matrices. The class of sufficient matrices is another generalization of  -matrices.[1]
-matrices.[1]
If the Jacobian of a function is a  -matrix, then the function is injective on any rectangular region of
-matrix, then the function is injective on any rectangular region of 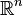 .
.
A related class of interest, particularly with reference to stability, is that of 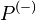 -matrices, sometimes also referred to as
-matrices, sometimes also referred to as 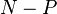 -matrices. A matrix
-matrices. A matrix  is a
is a 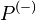 -matrix if and only if
-matrix if and only if 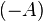 is a
is a  -matrix (similarly for
-matrix (similarly for 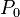 -matrices). Since
-matrices). Since 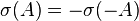 , the eigenvalues of these matrices are bounded away from the positive real axis.
, the eigenvalues of these matrices are bounded away from the positive real axis.
See also
Notes
- ↑ Csizmadia, Zsolt; Illés, Tibor (2006). "New criss-cross type algorithms for linear complementarity problems with sufficient matrices" (pdf). Optimization Methods and Software 21 (2): 247–266. doi:10.1080/10556780500095009. MR 2195759.
References
- Csizmadia, Zsolt; Illés, Tibor (2006). "New criss-cross type algorithms for linear complementarity problems with sufficient matrices" (pdf). Optimization Methods and Software 21 (2): 247–266. doi:10.1080/10556780500095009. MR 2195759.
- David Gale and Hukukane Nikaido, The Jacobian matrix and global univalence of mappings, Math. Ann. 159:81-93 (1965) doi:10.1007/BF01360282
- Li Fang, On the Spectra of
 - and
- and  -Matrices, Linear Algebra and its Applications 119:1-25 (1989)
-Matrices, Linear Algebra and its Applications 119:1-25 (1989) - R. B. Kellogg, On complex eigenvalues of
 and
and  matrices, Numer. Math. 19:170-175 (1972)
matrices, Numer. Math. 19:170-175 (1972)