P-group generation algorithm
In mathematics, specifically group theory, finite groups of prime power order 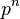 , for a fixed prime number
, for a fixed prime number  and varying integer exponents
and varying integer exponents  , are briefly called finite p-groups.
, are briefly called finite p-groups.
The p-group generation algorithm by M. F. Newman [1] and E. A. O'Brien [2] [3] is a recursive process for constructing the descendant tree of an assigned finite p-group which is taken as the root of the tree.
Lower exponent-p central series
For a finite p-group  , the lower exponent-p central series (briefly lower p-central series) of
, the lower exponent-p central series (briefly lower p-central series) of  is a descending series
is a descending series 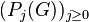 of characteristic subgroups of
of characteristic subgroups of  ,
defined recursively by
,
defined recursively by 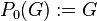 and
and 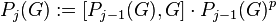 , for
, for 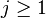 .
Since any non-trivial finite p-group
.
Since any non-trivial finite p-group 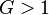 is nilpotent, there exists an integer
is nilpotent, there exists an integer 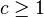 such that
such that 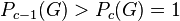 and
and 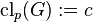 is called the exponent-p class (briefly p-class) of
is called the exponent-p class (briefly p-class) of  .
Only the trivial group
.
Only the trivial group 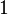 has
has 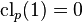 .
Generally, for any finite p-group
.
Generally, for any finite p-group  , its p-class can be defined as
, its p-class can be defined as 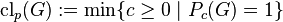 .
.
The complete series is given by 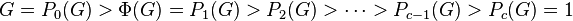 ,
,
since 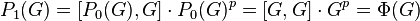 is the Frattini subgroup of
is the Frattini subgroup of  .
.
For the convenience of the reader and for pointing out the shifted numeration, we recall that
the (usual) lower central series of  is also a descending series
is also a descending series 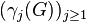 of characteristic subgroups of
of characteristic subgroups of  ,
defined recursively by
,
defined recursively by 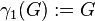 and
and 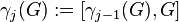 , for
, for 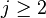 .
As above, for any non-trivial finite p-group
.
As above, for any non-trivial finite p-group 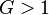 , there exists an integer
, there exists an integer 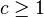 such that
such that 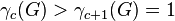 and
and 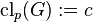 is called the nilpotency class of
is called the nilpotency class of  , whereas
, whereas 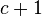 is called the index of nilpotency of
is called the index of nilpotency of  .
Only the trivial group
.
Only the trivial group 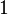 has
has 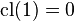 .
.
The complete series is given by 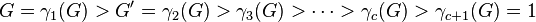 ,
,
since 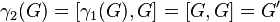 is the commutator subgroup or derived subgroup of
is the commutator subgroup or derived subgroup of  .
.
The following Rules should be remembered for the exponent-p class:
Let  be a finite p-group.
be a finite p-group.
- Rule:
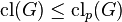 , since the
, since the 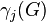 descend more quickly than the
descend more quickly than the 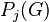 .
. - Rule:
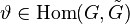 , for some group
, for some group 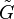
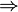
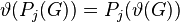 , for any
, for any 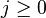 .
. - Rule: For any
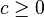 , the conditions
, the conditions 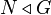 and
and 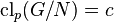 imply
imply 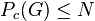 .
. - Rule: For any
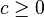 ,
, 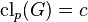
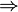
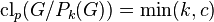 , for all
, for all 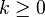 , and
, and 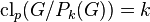 , for all
, for all 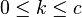 .
.
- Rule:
Parents and descendant trees
The parent 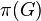 of a finite non-trivial p-group
of a finite non-trivial p-group 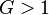 with exponent-p class
with exponent-p class 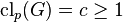 is defined as the quotient
is defined as the quotient 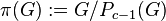 of
of  by the last non-trivial term
by the last non-trivial term 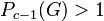 of the lower exponent-p central series of
of the lower exponent-p central series of  .
Conversely, in this case,
.
Conversely, in this case,  is called an immediate descendant of
is called an immediate descendant of 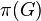 .
The p-classes of parent and immediate descendant are connected by
.
The p-classes of parent and immediate descendant are connected by 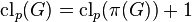 .
.
A descendant tree is a hierarchical structure
for visualizing parent-descendant relations
between isomorphism classes of finite p-groups.
The vertices of a descendant tree are isomorphism classes of finite p-groups.
However, a vertex will always be labelled by selecting a representative of the corresponding isomorphism class.
Whenever a vertex 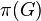 is the parent of a vertex
is the parent of a vertex  a directed edge of the descendant tree is defined by
a directed edge of the descendant tree is defined by 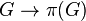 in the direction of the canonical projection
in the direction of the canonical projection 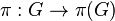 onto the quotient
onto the quotient 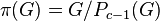 .
.
In a descendant tree, the concepts of parents and immediate descendants can be generalized.
A vertex  is a descendant of a vertex
is a descendant of a vertex  ,
and
,
and  is an ancestor of
is an ancestor of  ,
if either
,
if either  is equal to
is equal to  or there is a path
or there is a path 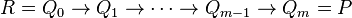 , with
, with 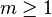 , of directed edges from
, of directed edges from  to
to  .
The vertices forming the path necessarily coincide with the iterated parents
.
The vertices forming the path necessarily coincide with the iterated parents 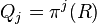 of
of  , with
, with 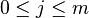 .
They can also be viewed as the successive quotients
.
They can also be viewed as the successive quotients 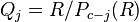 of p-class
of p-class 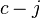 of
of  when the p-class of
when the p-class of  is given by
is given by 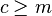 .
In particular, every non-trivial finite p-group
.
In particular, every non-trivial finite p-group 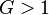 defines a maximal path (consisting of
defines a maximal path (consisting of  edges)
edges)
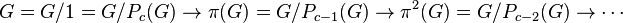
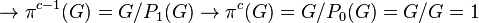 ending in the trivial group
ending in the trivial group 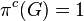 .
The last but one quotient of the maximal path of
.
The last but one quotient of the maximal path of  is the elementary abelian p-group
is the elementary abelian p-group 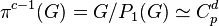 of rank
of rank 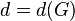 ,
where
,
where 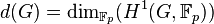 denotes the generator rank of
denotes the generator rank of  .
.
Generally, the descendant tree 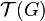 of a vertex
of a vertex  is the subtree of all descendants of
is the subtree of all descendants of  , starting at the root
, starting at the root  .
The maximal possible descendant tree
.
The maximal possible descendant tree 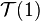 of the trivial group
of the trivial group 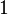 contains all finite p-groups and is exceptional,
since the trivial group
contains all finite p-groups and is exceptional,
since the trivial group 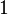 has all the infinitely many elementary abelian p-groups with varying generator rank
has all the infinitely many elementary abelian p-groups with varying generator rank 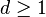 as its immediate descendants.
However, any non-trivial finite p-group (of order divisible by
as its immediate descendants.
However, any non-trivial finite p-group (of order divisible by  ) possesses only finitely many immediate descendants.
) possesses only finitely many immediate descendants.
p-covering group
Let  be a finite p-group with
be a finite p-group with  generators.
Our goal is to compile a complete list of pairwise non-isomorphic immediate descendants of
generators.
Our goal is to compile a complete list of pairwise non-isomorphic immediate descendants of  .
It turned out that all immediate descendants can be obtained as quotients of a certain extension
.
It turned out that all immediate descendants can be obtained as quotients of a certain extension 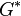 of
of  which is called the p-covering group of
which is called the p-covering group of  and can be constructed in the following manner.
and can be constructed in the following manner.
We can certainly find a presentation of  in the form of an exact sequence
in the form of an exact sequence 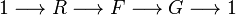 ,
where
,
where 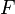 denotes the free group with
denotes the free group with  generators and
generators and 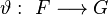 is an epimorphism with kernel
is an epimorphism with kernel 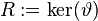 .
Then
.
Then 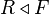 is a normal subgroup of
is a normal subgroup of 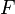 consisting of the defining relations for
consisting of the defining relations for 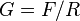 .
For elements
.
For elements 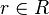 and
and 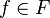 ,
the conjugate
,
the conjugate 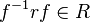 and thus also the commutator
and thus also the commutator 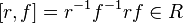 are contained in
are contained in  .
Consequently,
.
Consequently, 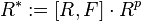 is a characteristic subgroup of
is a characteristic subgroup of  ,
and the p-multiplicator
,
and the p-multiplicator 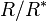 of
of  is an elementary abelian p-group, since
is an elementary abelian p-group, since 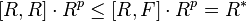 .
Now we can define the p-covering group of
.
Now we can define the p-covering group of  by
by 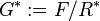 ,
and the exact sequence
,
and the exact sequence 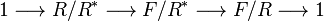 shows that
shows that 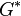 is an extension of
is an extension of  by the elementary abelian p-multiplicator.
We call
by the elementary abelian p-multiplicator.
We call 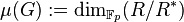 the p-multiplicator rank of
the p-multiplicator rank of  .
.
Let us assume now that the assigned finite p-group 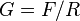 is of p-class
is of p-class 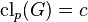 .
Then the conditions
.
Then the conditions 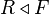 and
and 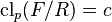 imply
imply 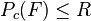 , according to Rule 3,
and we can define the nucleus of
, according to Rule 3,
and we can define the nucleus of  by
by 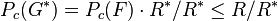 as a subgroup of the p-multiplicator.
Consequently, the nuclear rank
as a subgroup of the p-multiplicator.
Consequently, the nuclear rank 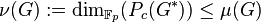 of
of  is bounded from above by the p-multiplicator rank.
is bounded from above by the p-multiplicator rank.
Allowable subgroups
As before, let  be a finite p-group with
be a finite p-group with  generators.
Any p-elementary abelian central extension
generators.
Any p-elementary abelian central extension 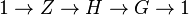 of
of  by a p-elementary abelian subgroup
by a p-elementary abelian subgroup 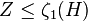 such that
such that 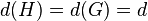 is a quotient of the p-covering group
is a quotient of the p-covering group 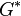 of
of  .
The reason is that there exists an epimorphism
.
The reason is that there exists an epimorphism 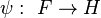 such that
such that 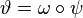 , where
, where 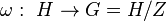 denotes the canonical projection.
Consequently, we have
denotes the canonical projection.
Consequently, we have 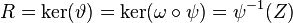 and thus
and thus 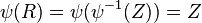 .
Further,
.
Further, 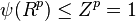 , since
, since  is p-elementary, and
is p-elementary, and 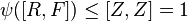 , since
, since  is central.
Together this shows that
is central.
Together this shows that 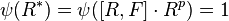 and thus
and thus 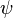 induces the desired epimorphism
induces the desired epimorphism 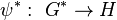 such that
such that 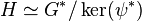 .
In particular, an immediate descendant
.
In particular, an immediate descendant  of
of  is a p-elementary abelian central extension
is a p-elementary abelian central extension 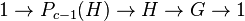 of
of  ,
since
,
since 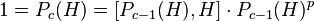 implies
implies 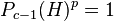 and
and 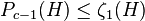 ,
where
,
where 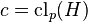 .
.
A subgroup 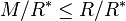 of the p-multiplicator of
of the p-multiplicator of  is called allowable
if it is given by the kernel
is called allowable
if it is given by the kernel 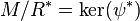 of an epimorphism
of an epimorphism 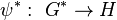 onto an immediate descendant
onto an immediate descendant  of
of  . An equivalent characterization is that
. An equivalent characterization is that 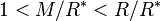 is a proper subgroup which supplements the nucleus
is a proper subgroup which supplements the nucleus
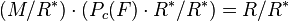 .
.
Therefore, the first part of our goal to compile a list of all immediate descendants of  is done,
when we have constructed all allowable subgroups of
is done,
when we have constructed all allowable subgroups of 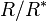 which supplement the nucleus
which supplement the nucleus 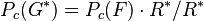 ,
where
,
where 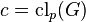 .
However, in general the list
.
However, in general the list 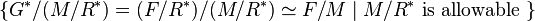 will be redundant,
due to isomorphisms
will be redundant,
due to isomorphisms 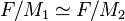 among the immediate descendants.
among the immediate descendants.
Orbits under extended automorphisms
Two allowable subgroups 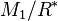 and
and 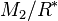 are called equivalent if the quotients
are called equivalent if the quotients 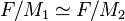 ,
that are the corresponding immediate descendants of
,
that are the corresponding immediate descendants of  , are isomorphic.
, are isomorphic.
Such an isomorphism 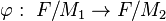 between immediate descendants of
between immediate descendants of 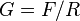 with
with 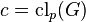 has the property that
has the property that
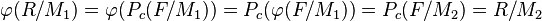 and thus induces an automorphism
and thus induces an automorphism 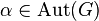 of
of  which can be extended to an automorphism
which can be extended to an automorphism 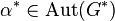 of the p-covering group
of the p-covering group 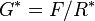 of
of  .
The restriction of this extended automorphism
.
The restriction of this extended automorphism 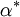 to the p-multiplicator
to the p-multiplicator 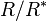 of
of  is determined uniquely by
is determined uniquely by  .
.
Since 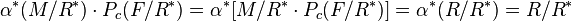 ,
each extended automorphism
,
each extended automorphism 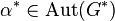 induces a permutation
induces a permutation 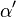 of the allowable subgroups
of the allowable subgroups 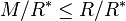 .
We define
.
We define 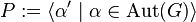 to be the permutation group generated by all permutations induced by automorphisms of
to be the permutation group generated by all permutations induced by automorphisms of  .
Then the map
.
Then the map 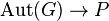 ,
, 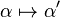 is an epimorphism
and the equivalence classes of allowable subgroups
is an epimorphism
and the equivalence classes of allowable subgroups 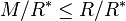 are precisely the orbits of allowable subgroups under the action of the permutation group
are precisely the orbits of allowable subgroups under the action of the permutation group  .
.
Eventually, our goal to compile a list 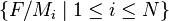 of all immediate descendants of
of all immediate descendants of  will be done,
when we select a representative
will be done,
when we select a representative 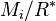 for each of the
for each of the  orbits of allowable subgroups of
orbits of allowable subgroups of 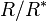 under the action of
under the action of  . This is precisely what the p-group generation algorithm does in a single step of the recursive procedure for constructing the descendant tree of an assigned root.
. This is precisely what the p-group generation algorithm does in a single step of the recursive procedure for constructing the descendant tree of an assigned root.
Capable p-groups and step sizes
A finite p-group  is called capable (or extendable) if it possesses at least one immediate descendant, otherwise it is terminal (or a leaf). The nuclear rank
is called capable (or extendable) if it possesses at least one immediate descendant, otherwise it is terminal (or a leaf). The nuclear rank 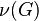 of
of  admits a decision about the capability of
admits a decision about the capability of  :
:
-
 is terminal if and only if
is terminal if and only if 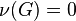 .
. -
 is capable if and only if
is capable if and only if 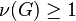 .
.
-
In the case of capability, 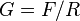 has immediate descendants of
has immediate descendants of 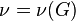 different step sizes
different step sizes 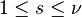 , in dependence on the index
, in dependence on the index 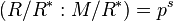 of the corresponding allowable subgroup
of the corresponding allowable subgroup 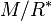 in the p-multiplicator
in the p-multiplicator 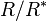 . When
. When  is of order
is of order 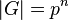 , then an immediate descendant of step size
, then an immediate descendant of step size  is of order
is of order 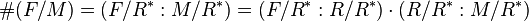
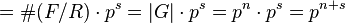 .
.
For the related phenomenon of multifurcation of a descendant tree at a vertex  with nuclear rank
with nuclear rank 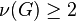 see the article on descendant trees.
see the article on descendant trees.
The p-group generation algorithm provides the flexibility to restrict the construction of immediate descendants to those of a single fixed step size 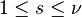 , which is very convenient in the case of huge descendant numbers (see the next section).
, which is very convenient in the case of huge descendant numbers (see the next section).
Numbers of immediate descendants
We denote the number of all immediate descendants, resp. immediate descendants of step size  , of
, of  by
by  , resp.
, resp. 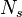 . Then we have
. Then we have 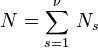 .
As concrete examples, we present some interesting finite metabelian p-groups with extensive sets of immediate descendants, using the SmallGroups identifiers and additionally pointing out the numbers
.
As concrete examples, we present some interesting finite metabelian p-groups with extensive sets of immediate descendants, using the SmallGroups identifiers and additionally pointing out the numbers 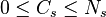 of capable immediate descendants in the usual format
of capable immediate descendants in the usual format 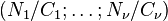 as given by actual implementations of the p-group generation algorithm in the computer algebra systems GAP and MAGMA.
as given by actual implementations of the p-group generation algorithm in the computer algebra systems GAP and MAGMA.
First, let  .
.
We begin with groups having abelianization of type 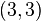 .
See Figure 4 in the article on descendant trees.
.
See Figure 4 in the article on descendant trees.
- The group
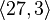 of coclass
of coclass 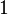 has ranks
has ranks 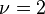 ,
, 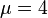 and descendant numbers
and descendant numbers 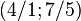 ,
, 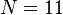 .
. - The group
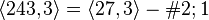 of coclass
of coclass 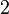 has ranks
has ranks 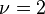 ,
, 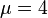 and descendant numbers
and descendant numbers 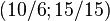 ,
, 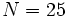 .
. - One of its immediate descendants, the group
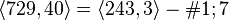 , has ranks
, has ranks 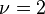 ,
, 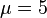 and descendant numbers
and descendant numbers 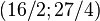 ,
, 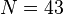 .
.
- The group
In contrast, groups with abelianization of type 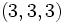 are partially located beyond the limit of computability.
are partially located beyond the limit of computability.
- The group
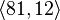 of coclass
of coclass 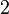 has ranks
has ranks 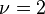 ,
, 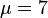 and descendant numbers
and descendant numbers 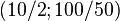 ,
, 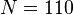 .
. - The group
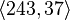 of coclass
of coclass 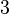 has ranks
has ranks 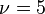 ,
, 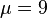 and descendant numbers
and descendant numbers 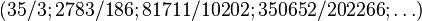 ,
, 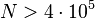 unknown.
unknown. - The group
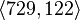 of coclass
of coclass 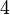 has ranks
has ranks 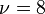 ,
, 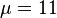 and descendant numbers
and descendant numbers 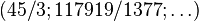 ,
, 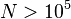 unknown.
unknown.
- The group
Next, let 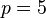 .
.
Corresponding groups with abelianization of type 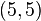 have bigger descendant numbers than for
have bigger descendant numbers than for  .
.
- The group
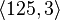 of coclass
of coclass 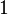 has ranks
has ranks 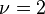 ,
, 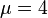 and descendant numbers
and descendant numbers 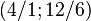 ,
, 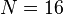 .
. - The group
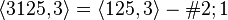 of coclass
of coclass 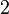 has ranks
has ranks 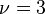 ,
, 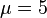 and descendant numbers
and descendant numbers 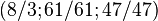 ,
, 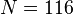 .
.
- The group
Schur multiplier
Via the isomorphism 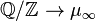 ,
, 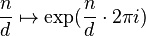 the quotient group
the quotient group 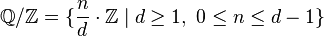 can be viewed as the additive analogue of the multiplicative group
can be viewed as the additive analogue of the multiplicative group 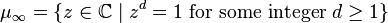 of all roots of unity.
of all roots of unity.
Let  be a prime number and
be a prime number and  be a finite p-group with presentation
be a finite p-group with presentation 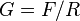 as in the previous section.
Then the second cohomology group
as in the previous section.
Then the second cohomology group 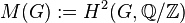 of the
of the  -module
-module 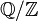 is called the Schur multiplier of
is called the Schur multiplier of  . It can also be interpreted as the quotient group
. It can also be interpreted as the quotient group 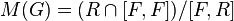 .
.
I. R. Shafarevich
[4]
has proved that the difference between the relation rank 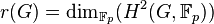 of
of  and the generator rank
and the generator rank 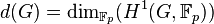 of
of  is given by the minimal number of generators of the Schur multiplier of
is given by the minimal number of generators of the Schur multiplier of  ,
that is
,
that is 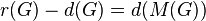 .
.
N. Boston and H. Nover
[5]
have shown that 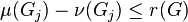 ,
for all quotients
,
for all quotients 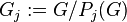 of p-class
of p-class 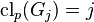 ,
, 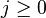 ,
of a pro-p group
,
of a pro-p group  with finite abelianization
with finite abelianization 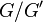 .
.
Furthermore, J. Blackhurst (in the appendix On the nucleus of certain p-groups of a paper by N. Boston, M. R. Bush and F. Hajir
[6])
has proved that a non-cyclic finite p-group  with trivial Schur multiplier
with trivial Schur multiplier 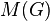 is a terminal vertex in the descendant tree
is a terminal vertex in the descendant tree 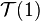 of the trivial group
of the trivial group 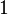 ,
that is,
,
that is, 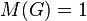
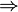
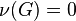 .
.
Examples
- A finite p-group
 has a balanced presentation
has a balanced presentation 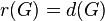 if and only if
if and only if 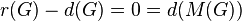 , that is, if and only if its Schur multiplier
, that is, if and only if its Schur multiplier 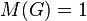 is trivial. Such a group is called a Schur group and it must be a leaf in the descendant tree
is trivial. Such a group is called a Schur group and it must be a leaf in the descendant tree 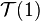 .
. - A finite p-group
 satisfies
satisfies 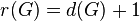 if and only if
if and only if 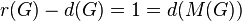 , that is, if and only if it has a non-trivial cyclic Schur multiplier
, that is, if and only if it has a non-trivial cyclic Schur multiplier 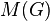 . Such a group is called a Schur+1 group.
. Such a group is called a Schur+1 group.
- A finite p-group
References
- ↑ Newman, M. F. (1977). Determination of groups of prime-power order. pp. 73-84, in: Group Theory, Canberra, 1975, Lecture Notes in Math., Vol. 573, Springer, Berlin.
- ↑ O'Brien, E. A. (1990). "The p-group generation algorithm". J. Symbolic Comput. 9: 677–698. doi:10.1016/s0747-7171(08)80082-x.
- ↑ Holt, D. F., Eick, B., O'Brien, E. A. (2005). Handbook of computational group theory. Discrete mathematics and its applications, Chapman and Hall/CRC Press.
- ↑ Shafarevich, I. R. (1964). "Extensions with given points of ramification (Russian)". Inst. Hautes \'Etudes Sci., Publ. Math. (English transl. in Amer. Math. Soc. Transl. (2) 59 (1966), 128-149) 18: 71–95.
- ↑ Boston, N., Nover, H. (2006). Computing pro-p Galois groups. Proceedings of the 7th Algorithmic Number Theory Symposium 2006, Lecture Notes in Computer Science 4076, 1-10, Springer, Berlin.
- ↑ Boston, N., Bush, M. R., Hajir, F. (2013). "Heuristics for p-class towers of imaginary quadratic fields". Math. Ann.: (preprint: arXiv:1111.4679v1 [math.NT], 2011).