P′′
| Paradigm | imperative, structured | ||||
|---|---|---|---|---|---|
| Designed by | Corrado Böhm | ||||
| First appeared | 1964 | ||||
| untyped | |||||
| |||||
P′′ is a primitive computer programming language created by Corrado Böhm[1][2] in 1964 to describe a family of Turing machines.
Definition
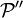 (hereafter written P′′) is formally defined as a set of words on the four-instruction alphabet {R, λ, (, )}, as follows:
(hereafter written P′′) is formally defined as a set of words on the four-instruction alphabet {R, λ, (, )}, as follows:
Syntax
- R and λ are words in P′′.
- If p and q are words in P′′, then pq is a word in P′′.
- If q is a word in P′′, then (q) is a word in P′′.
- Only words derivable from the previous three rules are words in P′′.
Semantics
- {a0, a1, ..., an}(n ≥ 1) is the tape-alphabet of a Turing machine with left-infinite tape, a0 being the blank symbol.
- R means move the tape-head rightward one cell (if any).
- λ means replace the current symbol ai by a(i+1) mod (n+1), and then move the tape-head leftward one cell.
- (q) means iterate q in a while loop, with condition that the current symbol is not a0.
- A program is a word in P′′. Execution of a program proceeds left-to-right, executing R, λ, and (q) as they are encountered, until there is nothing more to execute.
Relation to other programming languages
- P′′ was the first "GOTO-less" imperative structured programming language to be proven[1][2] Turing-complete.
- The brainfuck language (apart from its I/O commands) is a minor informal variation of P′′. Böhm[1] gives explicit P′′ programs for each of a set of basic functions sufficient to compute any computable function, using only (, ) and the four words r ≡ λR, r′ ≡ rn (rn means rrrrr...rr [n times]), L ≡ r′λ, R. These are the equivalents of the six respective brainfuck commands [, ], +, -, <, >. Note that since an+1 = a0, performing r ("increment" symbol in current cell) n times will wrap around so that the result is to "decrement" the symbol in the current cell by one (r′).
Example program
Böhm[1] gives the following program to compute the predecessor (x-1) of an integer x > 0:
R ( R ) L ( r' ( L ( L ) ) r' L ) R r
which translates directly to the equivalent brainfuck program
> [ > ] < [ − [ < [ < ] ] − < ] > +
The program expects an integer to be represented in bijective base-n notation, with a1, ..., an coding the digits 1,...,n, respectively, and to have an a0 before and after the digit-string. (E.g. in bijective base-2, the number eight would be encoded as a0a1a1a2a0, because 8 = 1*22 + 1*21 + 2*20.) At the beginning and end of the computation, the tape-head is on the a0 preceding the digit-string.
References
- ↑ 1.0 1.1 1.2 1.3 Böhm, C.: "On a family of Turing machines and the related programming language", ICC Bull. 3, 185-194, July 1964.
- ↑ 2.0 2.1 Böhm, C. and Jacopini, G.: "Flow diagrams, Turing machines and languages with only two formation rules", CACM 9(5), 1966. (Note: This is the most-cited paper on the structured program theorem.)