P²-irreducible
In mathematics, a 3-manifold is P2-irreducible if it is irreducible and contains no 2-sided 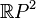 (real projective plane). An orientable manifold is P2-irreducible if and only if it is irreducible.[1] Every non-orientable P2-irreducible manifold is a Haken manifold.[2]
(real projective plane). An orientable manifold is P2-irreducible if and only if it is irreducible.[1] Every non-orientable P2-irreducible manifold is a Haken manifold.[2]
References
- ↑ Hazewinkel, Michiel (2001), Encyclopaedia of Mathematics, Supplement III, Volume 13, Springer, p. 183, ISBN 9781556080104.
- ↑ Rassias, George M.; Stratopoulos, George (1989), Geometry and Topology, World Scientific, p. 33, ISBN 9789971506780.