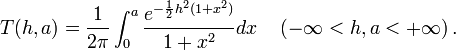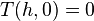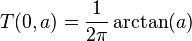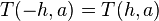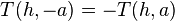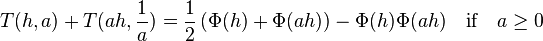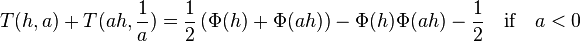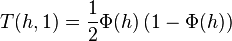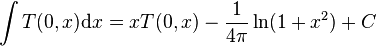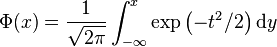Owen's T function

In mathematics, Owen's T function T(h, a), named after statistician Donald Bruce Owen, is defined by

T(h,a)=\frac{1}{2\pi}\int_{0}^{a} \frac{e^{-\frac{1}{2} h^2 (1+x^2)}}{1+x^2} dx \quad \left(-\infty < h, a < +\infty\right).

The function was first introduced by Owen in 1956.[1]

Applications

The function T(h, a) gives the probability of the event (X>h and 0<Y<a*X) where X and Y are independent standard normal random variables.

This function can be used to calculate bivariate normal distribution probabilities[2][3] and, from there, in the calculation of multivariate normal distribution probabilities.[4] It also frequently appears in various integrals involving Gaussian functions.

Computer algorithms for the accurate calculation of this function are available;[5] quadrature having been employed since the 1970s. [6]

Properties

T(h,0) = 0
T(0,a) = \frac{1}{2\pi} \arctan(a)
T(-h,a) = T(h,a)
T(h,-a) = -T(h,a)
T(h,a) + T(ah,\frac{1}{a}) = \frac{1}{2} \left(\Phi(h) + \Phi(ah)\right) - \Phi(h)\Phi(ah) \quad \mbox{if} \quad a \geq 0
T(h,a) + T(ah,\frac{1}{a}) = \frac{1}{2} \left(\Phi(h) + \Phi(ah)\right) - \Phi(h)\Phi(ah) - \frac{1}{2} \quad \mbox{if} \quad a < 0
T(h, 1) = \frac{1}{2} \Phi(h) \left(1 - \Phi(h)\right)
\int T(0,x) \mathrm{d}x = x T(0,x) - \frac{1}{4 \pi} \ln(1+x^2) + C

Here Φ(x) is the standard normal cumulative density function

\Phi(x) = \frac{1}{\sqrt{2\pi}} \int_{-\infty}^x \exp\left(-t^2 / 2\right) \mathrm{d}y

More properties can be found in the literature.[7]

References

  1. ↑ Owen, D B (1956). "Tables for computing bivariate normal probabilities". Annals of Mathematical Statistics, 27, 1075–1090.
  2. ↑ Sowden, R R and Ashford, J R (1969). "Computation of the bivariate normal integral". Applied Statististics, 18, 169–180.
  3. ↑ Donelly, T G (1973). "Algorithm 462. Bivariate normal distribution". Commun. Ass. Comput.Mach., 16, 638.
  4. ↑ Schervish, M H (1984). "Multivariate normal probabilities with error bound". Applied Statistics, 33, 81–94.
  5. ↑ Patefield, M. and Tandy, D. (2000) "Fast and accurate Calculation of Owen’s T-Function", Journal of Statistical Software, 5 (5), 1–25.
  6. ↑ JC Young and Christoph Minder. Algorithm AS 76
  7. ↑ Owen (1980)

Software

External links