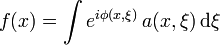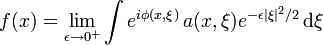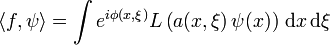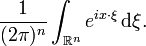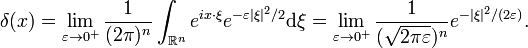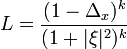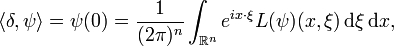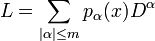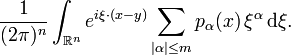Oscillatory integral
In mathematical analysis an oscillatory integral is a type of distribution. Oscillatory integrals make rigorous many arguments that, on a naive level, appear to use divergent integrals. It is possible to represent approximate solution operators for many differential equations as oscillatory integrals.
Definition
An oscillatory integral 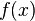 is written formally as
is written formally as
where 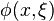 and
and 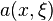 are functions defined on
are functions defined on 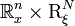 with the following properties.
with the following properties.
- 1) The function
 is real valued, positive homogeneous of degree 1, and infinitely differentiable away from
is real valued, positive homogeneous of degree 1, and infinitely differentiable away from 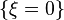 . Also, we assume that
. Also, we assume that  does not have any critical points on the support of
does not have any critical points on the support of  . Such a function,
. Such a function,  is usually called a phase function. In some contexts more general functions are considered, and still referred to as phase functions.
is usually called a phase function. In some contexts more general functions are considered, and still referred to as phase functions.
- 2) The function
 belongs to one of the symbol classes
belongs to one of the symbol classes 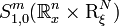 for some
for some 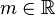 . Intuitively, these symbol classes generalize the notion of positively homogeneous functions of degree
. Intuitively, these symbol classes generalize the notion of positively homogeneous functions of degree  . As with the phase function
. As with the phase function  , in some cases the function
, in some cases the function  is taken to be in more general, or just different, classes.
is taken to be in more general, or just different, classes.
When 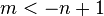 the formal integral defining
the formal integral defining 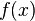 converges for all
converges for all  and there is no need for any further discussion of the definition of
and there is no need for any further discussion of the definition of 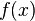 . However, when
. However, when 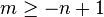 the oscillatory integral is still defined as a distribution on
the oscillatory integral is still defined as a distribution on 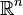 even though the integral may not converge. In this case the distribution
even though the integral may not converge. In this case the distribution 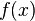 is defined by using the fact that
is defined by using the fact that 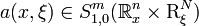 may be approximated by functions that have exponential decay in
may be approximated by functions that have exponential decay in 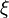 . One possible way to do this is by setting
. One possible way to do this is by setting
where the limit is taken in the sense of tempered distributions. Using integration by parts it is possible to show that this limit is well defined, and that there exists a differential operator  such that the resulting distribution
such that the resulting distribution 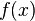 acting on any
acting on any 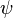 in the Schwartz space is given by
in the Schwartz space is given by
where this integral converges absolutely. The operator  is not uniquely defined, but can be chosen in such a way that depends only on the phase function
is not uniquely defined, but can be chosen in such a way that depends only on the phase function  , the order
, the order  of the symbol
of the symbol  , and
, and  . In fact, given any integer
. In fact, given any integer  it is possible to find an operator
it is possible to find an operator  so that the integrand above is bounded by
so that the integrand above is bounded by 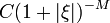 for
for 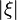 sufficiently large. This is the main purpose of the definition of the symbol classes.
sufficiently large. This is the main purpose of the definition of the symbol classes.
Examples
Many familiar distributions can be written as oscillatory integrals.
- 1) The Fourier inversion theorem implies that the delta function,
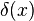 is equal to
is equal to
- If we apply the first method of defining this oscillatory integral from above, as well as the Fourier transform of the Gaussian, we obtain a well known sequence of functions which approximate the delta function:
- An operator
 in this case is given for example by
in this case is given for example by
- where
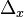 is the Laplacian with respect to the
is the Laplacian with respect to the  variables, and
variables, and  is any integer greater than
is any integer greater than 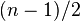 . Indeed, with this
. Indeed, with this  we have
we have
- and this integral converges absolutely.
- 2) The Schwartz kernel of any differential operator can be written as an oscillatory integral. Indeed if
- where
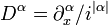 , then the kernel of
, then the kernel of  is given by
is given by
Relation to Lagrangian distributions
Any Lagrangian distribution can be represented locally by oscillatory integrals (see Hörmander (1983)). Conversely any oscillatory integral is a Lagrangian distribution. This gives a precise description of the types of distributions which may be represented as oscillatory integrals.
See also
References
- Hörmander, Lars (1983), The Analysis of Linear Partial Differential Operators IV, Springer-Verlag, ISBN 0-387-13829-3
- Hörmander, Lars (1971), "Fourier integral operators I", Acta Math. 127: 79–183, doi:10.1007/bf02392052