Orthocentroidal circle

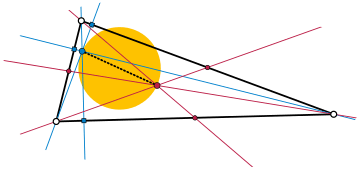
A triangle (black), its orthocenter (blue), its centroid (red), and its orthocentroidal disk (yellow)

In geometry, the orthocentroidal circle of a non-equilateral triangle is the circle that has the triangle's orthocenter and its centroid at opposite ends of a diameter. Guinand showed in 1984 that the triangle's incenter must lie in the interior of the orthocentroidal circle, but not coinciding with the nine-point center; that is, it must fall in the open orthocentroidal disk punctured at the nine-point center.[1][2][3][4] [5]:pp. 451–452

Furthermore,[2] the Fermat point, the Gergonne point, and the symmedian point are in the open orthocentroidal disk punctured at its own center (and could be at any point therein), while the second Fermat point is in the exterior of the orthocentroidal circle (and likewise could be at any such point). The set of potential locations of one or the other of the Brocard points is also the open orthocentroidal disk.[6]

References

  1. ↑ Guinand, Andrew P. (1984), "Euler lines, tritangent centers, and their triangles", American Mathematical Monthly 91 (5): 290–300, JSTOR 2322671.
  2. ↑ 2.0 2.1 Bradley, Christopher J.; Smith, Geoff C. (2006), "The locations of triangle centers", Forum Geometricorum 6: 57–70.
  3. ↑ Stern, Joseph (2007), "Euler’s triangle determination problem", Forum Geometricorum 7: 1–9.
  4. ↑ Franzsen, William N. (2011), "The distance from the incenter to the Euler line", Forum Geometricorum 11: 231–236.
  5. ↑ Leversha, Gerry; Smith, G. C. (November 2007), "Euler and triangle geometry", Mathematical Gazette 91 (522): 436–452, JSTOR 40378417.
  6. ↑ Bradley, Christopher J.; Smith, Geoff C. (2006), "The locations of the Brocard points", Forum Geometricorum 6: 71–77.