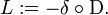Ornstein–Uhlenbeck operator
In mathematics, the Ornstein–Uhlenbeck operator is a generalization of the Laplace operator to an infinite-dimensional setting. The Ornstein–Uhlenbeck operator plays a significant role in the Malliavin calculus.
Introduction: the finite-dimensional picture
The Laplacian
Consider the gradient operator ∇ acting on scalar functions f : Rn → R; the gradient of a scalar function is a vector field v = ∇f : Rn → Rn. The divergence operator div, acting on vector fields to produce scalar fields, is the adjoint operator to ∇. The Laplace operator Δ is then the composition of the divergence and gradient operators:
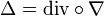 ,
,
acting on scalar functions to produce scalar functions. Note that A = −Δ is a positive operator, whereas Δ is a dissipative operator.
Using spectral theory, one can define a square root (1 − Δ)1/2 for the operator (1 − Δ). This square root satisfies the following relation involving the Sobolev H1-norm and L2-norm for suitable scalar functions f:
The Ornstein–Uhlenbeck operator
Often, when working on Rn, one works with respect to Lebesgue measure, which has many nice properties. However, remember that the aim is to work in infinite-dimensional spaces, and it is a fact that there is no infinite-dimensional Lebesgue measure. Instead, if one is studying some separable Banach space E, what does make sense is a notion of Gaussian measure; in particular, the abstract Wiener space construction makes sense.
To get some intuition about what can be expected in the infinite-dimensional setting, consider standard Gaussian measure γn on Rn: for Borel subsets A of Rn,
This makes (Rn, B(Rn), γn) into a probability space; E will denote expectation with respect to γn.
The gradient operator ∇ acts on a (differentiable) function φ : Rn → R to give a vector field ∇φ : Rn → Rn.
The divergence operator δ (to be more precise, δn, since it depends on the dimension) is now defined to be the adjoint of ∇ in the Hilbert space sense, in the Hilbert space L2(Rn, B(Rn), γn; R). In other words, δ acts on a vector field v : Rn → Rn to give a scalar function δv : Rn → R, and satisfies the formula
On the left, the product is the pointwise Euclidean dot product of two vector fields; on the right, it is just the pointwise multiplication of two functions. Using integration by parts, one can check that δ acts on a vector field v with components vi, i = 1, ..., n, as follows:
The change of notation from “div” to “δ” is for two reasons: first, δ is the notation used in infinite dimensions (the Malliavin calculus); secondly, δ is really the negative of the usual divergence.
The (finite-dimensional) Ornstein–Uhlenbeck operator L (or, to be more precise, Lm) is defined by
with the useful formula that for any f and g smooth enough for all the terms to make sense,
The Ornstein–Uhlenbeck operator L is related to the usual Laplacian Δ by
The Ornstein–Uhlenbeck operator for a separable Banach space
Consider now an abstract Wiener space E with Cameron-Martin Hilbert space H and Wiener measure γ. Let D denote the Malliavin derivative. The Malliavin derivative D is an unbounded operator from L2(E, γ; R) into L2(E, γ; H) – in some sense, it measures “how random” a function on E is. The domain of D is not the whole of L2(E, γ; R), but is a dense linear subspace, the Watanabe-Sobolev space, often denoted by 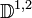 (once differentiable in the sense of Malliavin, with derivative in L2).
(once differentiable in the sense of Malliavin, with derivative in L2).
Again, δ is defined to be the adjoint of the gradient operator (in this case, the Malliavin derivative is playing the role of the gradient operator). The operator δ is also known the Skorokhod integral, which is an anticipating stochastic integral; it is this set-up that gives rise to the slogan “stochastic integrals are divergences”. δ satisfies the identity
for all F in 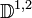 and v in the domain of δ.
and v in the domain of δ.
Then the Ornstein–Uhlenbeck operator for E is the operator L defined by
References
- Ocone, Daniel L. (1988). "A guide to the stochastic calculus of variations". Stochastic analysis and related topics (Silivri, 1986). Lecture Notes in Math. 1316. Berlin: Springer. pp. 1–79. MR 953793
- Sanz-Solé, Marta (2008). "Applications of Malliavin Calculus to Stochastic Partial Differential Equations (Lectures given at Imperial College London, 7–11 July 2008)". Retrieved 2008-07-09.
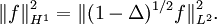
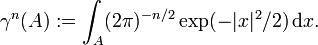
![\mathbb{E} \big[ \nabla f \cdot v \big] = \mathbb{E} \big[ f \delta v \big].](../I/m/c7e743395edc986398f32b699bb7f35c.png)
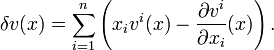
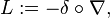
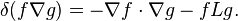
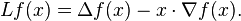
![\mathbb{E} \big[ \langle \mathrm{D} F, v \rangle_{H} \big] = \mathbb{E} \big[ F \delta v \big]](../I/m/943893cb743ed439b5852b4e40632072.png)