Ore algebra
In computer algebra, an Ore algebra is a special kind of iterated Ore extension that can be used to represent linear functional operators, including linear differential and/or recurrence operators.[1] The concept is named after Øystein Ore.
Definition
Let  be a (commutative) field and
be a (commutative) field and ![A = K[x_1, \ldots, x_s]](../I/m/095052b631e96156f87d851d17fcc873.png) be a commutative polynomial ring (with
be a commutative polynomial ring (with 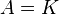 when
when 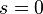 ). The iterated skew polynomial ring
). The iterated skew polynomial ring ![A[\partial_1; \sigma_1, \delta_1] \cdots [\partial_r; \sigma_r, \delta_r]](../I/m/c8bfc079041a2e8905abccbb62a2ff41.png) is called an Ore algebra when the
is called an Ore algebra when the 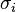 and
and 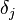 commute for
commute for 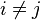 , and satisfy
, and satisfy 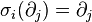 ,
, 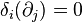 for
for 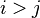 .
.
Properties
Ore algebras satisfy the Ore condition, and thus can be embedded in a (skew) field of fractions.
The constraint of commutation in the definition makes Ore algebras have a non-commutative generalization theory of Gröbner basis for their left ideals.
References
- ↑ Chyzak, Frédéric; Salvy, Bruno (1998). "Non-commutative Elimination in Ore Algebras Proves Multivariate Identities". Journal of Symbolic Computation (Elsevier) 26 (2): 187–227. doi:10.1006/jsco.1998.0207.