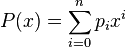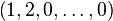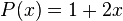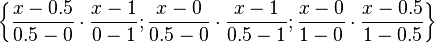Order of a polynomial

In mathematics, the order of a polynomial may have several meanings, depending on the context.

Order has been used to denoted the degree of a polynomial. Nowadays, this terminology is rarely used.
Order may refer to the order of the polynomial, viewed as a power series, that is the degree of its nonzero monomial of lowest degree.
The meaning in this article.

In this article, the order of a polynomial, relative to a particular set of polynomial basis functions spanning the polynomial vector space in which a given polynomial is included, is the highest degree among those basis functions used to express the polynomial.^[1]

Example

Consider the following polynomial:

P(x) = \sum^n_{i=0} p_i x^i

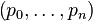where $\left(p_0, \ldots, p_n\right)$ are the polynomial coefficients and 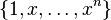$\left\{1, x, \ldots, x^n\right\}$ the set of basis functions which span the polynomial vector space.

If the polynomial coefficients are:

\left(1, 2, 0, \ldots, 0\right)

under this polynomial vector space, 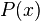$P(x)$ is expressed as follows:

P(x) = 1 + 2x

The degree of this polynomial would be 1. Yet, due to the set of basis functions which is used to define this polynomial, its order would be $n$ .

Now, consider the same polynomial expressed in Lagrange form. If this polynomial is defined as a linear combination of the following set of basis functions:

\left\{ \frac{x - 0.5}{0.5-0}\cdot\frac{x-1}{0-1} ; \frac{x-0}{0.5-0}\cdot\frac{x-1}{0.5-1}; \frac{x-0}{1-0}\cdot\frac{x-0.5}{1-0.5} \right\}

then, the polynomial coefficients would be:

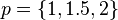p=\left\{1, 1.5, 2\right\}

The degree of this polynomial would still be 1, but as the highest degree of the Lagrangian basis functions is 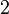$2$ , then the order of this polynomial is 2.

References

↑ de Boor, Carl (2001). A Practical Guide to Splines. Springer. p. 1. ISBN 0-387-95366-3.

Order of a polynomial

Example

See also

References