Optical scalars
In general relativity, optical scalars refer to a set of three scalar functions 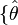 (expansion),
(expansion), 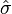 (shear) and
(shear) and 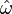 (twist/rotation/vorticity)
(twist/rotation/vorticity)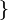 describing the propagation of a geodesic null congruence.[1][2][3][4][5]
describing the propagation of a geodesic null congruence.[1][2][3][4][5]
In fact, these three scalars 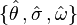 can be defined for both timelike and null geodesic congruences in an identical spirit, but they are called "optical scalars" only for the null case. Also, it is their tensorial predecessors
can be defined for both timelike and null geodesic congruences in an identical spirit, but they are called "optical scalars" only for the null case. Also, it is their tensorial predecessors 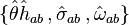 that are adopted in tensorial equations, while the scalars
that are adopted in tensorial equations, while the scalars 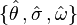 mainly show up in equations written in the language of Newman–Penrose formalism.
mainly show up in equations written in the language of Newman–Penrose formalism.
Definitions: expansion, shear and twist
For geodesic timelike congruences
Denote the tangent vector field of an observer's worldline (in a timelike congruence) as 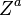 , and then one could construct induced "spatial metrics" that
, and then one could construct induced "spatial metrics" that
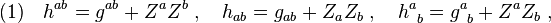
where 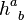 works as a spatially projecting operator. Use
works as a spatially projecting operator. Use 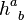 to project the coordinate covariant derivative
to project the coordinate covariant derivative 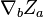 and one obtains the "spatial" auxiliary tensor
and one obtains the "spatial" auxiliary tensor 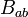 ,
,
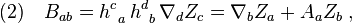
where  represents the four-acceleration, and
represents the four-acceleration, and  is purely spatial in the sense that
is purely spatial in the sense that  . Specifically for an observer with a "geodesic" timelike worldline, we have
. Specifically for an observer with a "geodesic" timelike worldline, we have
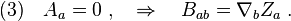
Now decompose 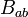 into the symmetric part
into the symmetric part 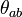 and
and 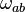 ,
,
![(4)\quad \theta_{ab}=B_{(ab)}\;,\quad \omega_{ab}=B_{[ab]}\;.](../I/m/59c724dcab75cf76ab7386a82264b4a8.png)
![\omega_{ab}=B_{[ab]}](../I/m/63b73366c12a9c2b85b855c12b210f3a.png) is trace-free (
is trace-free (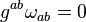 ) while
) while 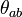 is of nonzero trace,
is of nonzero trace, 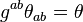 . Thus, the symmetric part
. Thus, the symmetric part 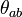 can be further rewritten into its trace and trace-free part,
can be further rewritten into its trace and trace-free part,
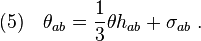
Hence, all in all we have
![(6)\quad B_{ab}=\frac{1}{3}\theta h_{ab} +\sigma_{ab}+\omega_{ab}\;,\quad \theta=g^{ab}\theta_{ab}=g^{ab}B_{(ab)}\;,\quad \sigma_{ab}=\theta_{ab}-\frac{1}{3}\theta h_{ab}\;,\quad \omega_{ab}=B_{[ab]}\;.](../I/m/3f95c0b70d66dba7e89783fe954c36d2.png)
For geodesic null congruences
Now, consider a geodesic null congruence with tangent vector field 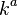 . Similar to the timelike situation, we also define
. Similar to the timelike situation, we also define
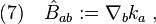
which can be decomposed into
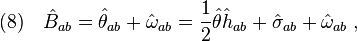
where
![(9)\quad \hat\theta_{ab}=\hat B_{(ab)}\;,\quad \hat\theta=\hat h^{ab} \hat B_{ab}\;,\quad \hat\sigma_{ab}=\hat B_{(ab)}-\frac{1}{2}\hat\theta \hat h_{ab}\;,\quad \hat\omega_{ab}=\hat B_{[ab]}\;.](../I/m/1d47af0cb19011a81facf73cd3cd7f8c.png)
Here, "hatted" quantities are utilized to stress that these quantities for null congruences are two-dimensional as opposed to the three-dimensional timelike case. However, if we only discuss null congruences in a paper, the hats can be omitted for simplicity.
Definitions: optical scalars for null congruences
The optical scalars 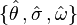 [1][2][3][4][5] come straightforwardly from "scalarization" of the tensors
[1][2][3][4][5] come straightforwardly from "scalarization" of the tensors 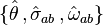 in Eq(9).
in Eq(9).
The expansion of a geodesic null congruence is defined by (where for clearance we will adopt another standard symbol "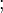 " to denote the covariant derivative
" to denote the covariant derivative 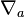 )
)
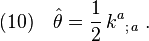
As shown in the article "Expansion rate of a null congruence", the outgoing and ingoing expansion rates, denoted by 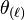 and
and 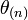 respectively, are defined by
respectively, are defined by
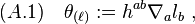
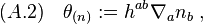
where 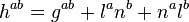 represents the induced metric. Also,
represents the induced metric. Also, 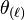 and
and 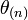 can be calculated via
can be calculated via
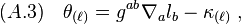
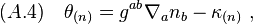
where 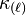 and
and 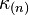 are respectively the outgoing and ingoing non-affinity coefficients defined by
are respectively the outgoing and ingoing non-affinity coefficients defined by
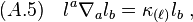
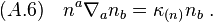
Moreover, in the language of Newman–Penrose formalism with the convention 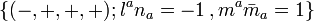 , we have
, we have
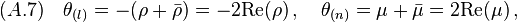
As we can see, for a geodesic null congruence, the optical scalar 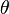 plays the same role with the expansion rates
plays the same role with the expansion rates 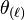 and
and 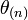 . Hence, for a geodesic null congruence,
. Hence, for a geodesic null congruence, 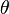 will be equal to either
will be equal to either 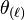 or
or 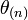 .
.
The shear of a geodesic null congruence is defined by
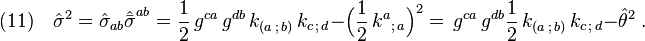
The twist of a geodesic null congruence is defined by
![(12)\quad {\hat\omega}^2 =\frac{1}{2}\,k_{[a\,;\,b]}\,k^{a\,;\,b} =g^{ca}\,g^{db}\,k_{[a\,;\,b]}\,k_{c\,;\,d}\;.](../I/m/cc986cab902ea20c4e4b52845d5450ef.png)
In practice, a geodesic null congruence is usually defined by either its outgoing (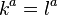 ) or ingoing (
) or ingoing (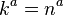 ) tangent vector field (which are also its null normals). Thus, we obtain two sets of optical scalars
) tangent vector field (which are also its null normals). Thus, we obtain two sets of optical scalars 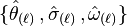 and
and 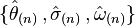 , which are defined with respect to
, which are defined with respect to 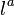 and
and 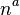 , respectively.
, respectively.
Applications in decomposing the propagation equations
For a geodesic timelike congruence
The propagation (or evolution) of 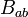 for a geodesic timelike congruence along
for a geodesic timelike congruence along 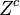 respects the following equation,
respects the following equation,
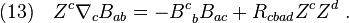
Take the trace of Eq(13) by contracting it with 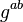 , and Eq(13) becomes
, and Eq(13) becomes
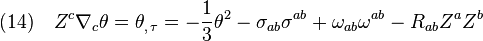
in terms of the quantities in Eq(6). Moreover, the trace-free, symmetric part of Eq(13) is
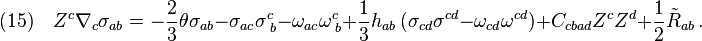
Finally, the antisymmetric component of Eq(13) yields
![(16)\quad Z^c\nabla_c \omega_{ab}=-\frac{2}{3}\theta\omega_{ab}-2\sigma^c_{\;[b}\omega_{a]c}\;.](../I/m/dcb6cc585b0d45522e499dc4f2acda0e.png)
For a geodesic null congruence
A (generic) geodesic null congruence obeys the following propagation equation,
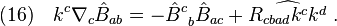
With the definitions summarized in Eq(9), Eq(14) could be rewritten into the following componential equations,
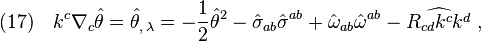

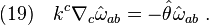
For a restricted geodesic null congruence
For a geodesic null congruence restricted on a null hypersurface, we have
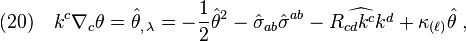
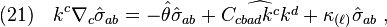
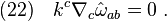
Spin coefficients, Raychaudhuri's equation and optical scalars
For a better understanding of the previous section, we will briefly review the meanings of relevant NP spin coefficients in depicting null congruences.[1] The tensor form of Raychaudhuri's equation[6] governing null flows reads
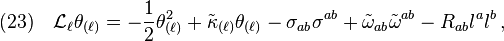
where 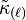 is defined such that
is defined such that 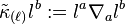 . The quantities in Raychaudhuri's equation are related with the spin coefficients via
. The quantities in Raychaudhuri's equation are related with the spin coefficients via
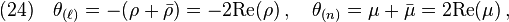
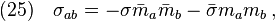
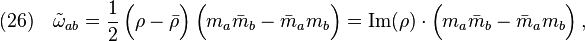
where Eq(24) follows directly from 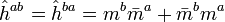 and
and
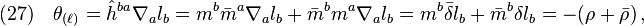
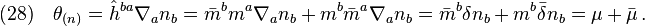
See also
References
- ↑ 1.0 1.1 1.2 Eric Poisson. A Relativist's Toolkit: The Mathematics of Black-Hole Mechanics. Cambridge: Cambridge University Press, 2004. Chapter 2.
- ↑ 2.0 2.1 Hans Stephani, Dietrich Kramer, Malcolm MacCallum, Cornelius Hoenselaers, Eduard Herlt. Exact Solutions of Einstein's Field Equations. Cambridge: Cambridge University Press, 2003. Chapter 6.
- ↑ 3.0 3.1 Subrahmanyan Chandrasekhar. The Mathematical Theory of Black Holes. Oxford: Oxford University Press, 1998. Section 9.(a).
- ↑ 4.0 4.1 Jeremy Bransom Griffiths, Jiri Podolsky. Exact Space-Times in Einstein's General Relativity. Cambridge: Cambridge University Press, 2009. Section 2.1.3.
- ↑ 5.0 5.1 P Schneider, J Ehlers, E E Falco. Gravitational Lenses. Berlin: Springer, 1999. Section 3.4.2.
- ↑ Sayan Kar, Soumitra SenGupta. The Raychaudhuri equations: a brief review. Pramana, 2007, 69(1): 49-76. [arxiv.org/abs/gr-qc/0611123v1 gr-qc/0611123]