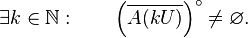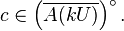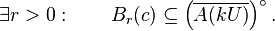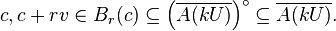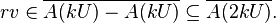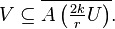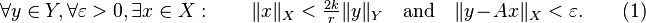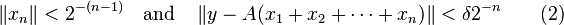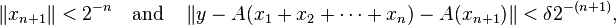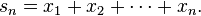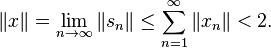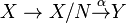Open mapping theorem (functional analysis)

In functional analysis, the open mapping theorem, also known as the Banach–Schauder theorem (named after Stefan Banach and Juliusz Schauder), is a fundamental result which states that if a continuous linear operator between Banach spaces is surjective then it is an open map. More precisely, (Rudin 1973, Theorem 2.11):

Open Mapping Theorem. If X and Y are Banach spaces and A : X → Y is a surjective continuous linear operator, then A is an open map (i.e. if U is an open set in X, then A(U) is open in Y).

The proof uses the Baire category theorem, and completeness of both X and Y is essential to the theorem. The statement of the theorem is no longer true if either space is just assumed to be a normed space, but is true if X and Y are taken to be Fréchet spaces.

Consequences

The open mapping theorem has several important consequences:

If A : X → Y is a bijective continuous linear operator between the Banach spaces X and Y, then the inverse operator A⁻¹ : Y → X is continuous as well (this is called the bounded inverse theorem). (Rudin 1973, Corollary 2.12)
If A : X → Y is a linear operator between the Banach spaces X and Y, and if for every sequence (x_n) in X with x_n → 0 and Ax_n → y it follows that y = 0, then A is continuous (the closed graph theorem). (Rudin 1973, Theorem 2.15)

Proof

Suppose A : X → Y is a surjective continuous linear operator. In order to prove that A is an open map, it is sufficient to show that A maps the open unit ball in X to a neighborhood of the origin of Y.

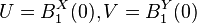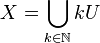Let $U=B_1^X(0), V=B_1^Y(0)$ . Then $X=\bigcup_{k\in\mathbb{N}}kU$ .

Since A is surjective:

Y=A(X)=A\left(\bigcup_{k \in \mathbb{N}} kU\right) = \bigcup_{k \in \mathbb{N}} A(kU).

But Y is Banach so by Baire's category theorem

\exists k \in \mathbb{N}: \qquad \left (\overline{A(kU)} \right )^\circ \neq \varnothing.

Let

c \in \left (\overline{A(kU)} \right )^\circ.

Since:

\left (\overline{A(kU)} \right )^{\circ\circ}= \left (\overline{A(kU)} \right )^\circ

we have:

\exists r>0: \qquad B_r(c) \subseteq \left (\overline{A(kU)} \right )^\circ.

Let v ∈ V, then

c, c+rv \in B_r(c)\subseteq \left (\overline{A(kU)} \right )^\circ \subseteq \overline{A(kU)}.

By continuity of addition, the difference

rv\in\overline{A(kU)-A(kU)}\subseteq \overline{A(2kU)}.

And A is linear so

V\subseteq \overline{A\left (\tfrac{2k}{r}U \right )}.

It follows that

\forall y \in Y, \forall \varepsilon > 0, \exists x \in X: \qquad \|x\|_X< \tfrac{2k}{r} \|y\|_Y \quad \text{and} \quad \|y - Ax\|_X< \varepsilon. \qquad (1)

Fix $y \in δV$ , by (1), there is some $x 1$ with $|| x 1 || < 1$ and $|| y - Ax 1 || < δ / 2$ . Define a sequence {x_n} inductively as follows. Assume:

\|x_n\|< 2^{-(n-1)} \quad \text{and} \quad \left\|y - A(x_1+x_2+ \cdots +x_n) \right \| < \delta 2^{-n} \qquad (2)

by (1) we can pick $x n +1$ so that:

\|x_{n+1}\|< 2^{-n} \quad \text{and} \quad \left \|y - A(x_1+x_2+ \cdots +x_n) - A(x_{n+1}) \right \| < \delta 2^{-(n+1)},

so (2) is satisfied for $x n +1$ . Let

s_n=x_1+x_2+ \cdots + x_n.

From the first inequality in (2), {s_n} is a Cauchy sequence, and since X is complete, s_n converges to some $x \in X$ . By (2), the sequence $As n$ tends to y, and so $Ax = y$ by continuity of A. Also,

\|x\|=\lim_{n \to \infty} \|s_n\| \leq \sum_{n=1}^\infty \|x_n\| < 2.

This shows that every $y \in δV$ belongs to $A (2 U)$ , or equivalently, that the image A(U) of the unit ball in X contains the open ball $δ / 2 V \subset Y$ . Hence, A(U) is a neighborhood of 0 in Y, and this concludes the proof.

Generalizations

Local convexity of X or Y is not essential to the proof, but completeness is: the theorem remains true in the case when X and Y are F-spaces. Furthermore, the theorem can be combined with the Baire category theorem in the following manner (Rudin, Theorem 2.11):

Let X be a F-space and Y a topological vector space. If $A : X \to Y$ is a continuous linear operator, then either A(X) is a meager set in Y, or A(X) = Y. In the latter case, A is an open mapping and Y is also an F-space.

Furthermore, in this latter case if N is the kernel of A, then there is a canonical factorization of A in the form

X\to X/N \overset{\alpha}{\to} Y

where $X / N$ is the quotient space (also an F-space) of X by the closed subspace N. The quotient mapping $X \to X / N$ is open, and the mapping α is an isomorphism of topological vector spaces (Dieudonné, 12.16.8).

The open mapping theorem can also be stated as^[1]

Let X and Y be two F-spaces. Then every continuous linear map of X onto Y is a TVS homomorphism.

where a linear map $u : X \to Y$ is a topological vector space homomorphism if the induced map 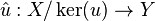$\hat{u} : X/\ker(u) \to Y$ is a TVS-isomorphism onto its image.

References

↑ Trèves (1995), p. 170

Rudin, Walter (1973), Functional Analysis, McGraw-Hill, ISBN 0-07-054236-8
Dieudonné, Jean (1970), Treatise on Analysis, Volume II, Academic Press
Trèves, François (1995), Topological Vector Spaces, Distributions and Kernels, Academic Press, Inc., pp. 166, 170, ISBN 0-486-45352-9

This article incorporates material from Proof of open mapping theorem on PlanetMath, which is licensed under the Creative Commons Attribution/Share-Alike License.

Functional analysis

Set / subset types	Absolutely convex Absorbing Balanced Bounded Convex Radial Star-shaped Symmetric Linear cone (subset) Convex cone (subset)

TVS types	Banach Barrelled Bornological Brauner F-space Finite-dimensional Fréchet (tame) Hilbert LF-space Locally convex Mackey Montel Nuclear Normed (norm) Quasinormed Reflexive Riesz Smith Stereotype Webbed Topological tensor product (of Hilbert spaces)

Mapping topologies	Dual Dual space Operator Strong (polar operator) Ultrastrong Weak (operator) Ultraweak Uniform convergence

Linear operators	Adjoint Bilinear (form) Bounded / Unbounded Closed Continuous / Discontinuous Compact Fredholm Hilbert–Schmidt Functionals (positive) Normal Nuclear Self-adjoint Strictly singular Trace class Transpose Unitary

Set operations	Algebraic interior (core) Interior Minkowski addition Polar

Banach algebras	C-algebras Spectrum (C-algebra radius) Spectral theory

Theorems	Banach–Alaoglu Banach–Saks Banach–Mazur Bessel's inequality Cauchy–Schwarz inequality Closed range Closed graph Eberlein–Šmulian Freudenthal spectral Gelfand–Mazur Goldstine Hahn–Banach (hyperplane separation) Kakutani fixed-point Lomonosov's invariant subspace Mackey–Arens Mazur's lemma M. Riesz extension Open mapping Parseval's identity Schauder fixed-point

Analysis	Bochner space Differentiation in Fréchet spaces Derivatives (Fréchet Gâteaux functional holomorphic) Integrals (Bochner Dunford Gelfand–Pettis regulated weak) Functional calculus (Borel continuous holomorphic) Inverse function theorem (Nash–Moser theorem) Vector measure