One-way analysis of variance
In statistics, one-way analysis of variance (abbreviated one-way ANOVA) is a technique used to compare means of three or more samples (using the F distribution). This technique can be used only for numerical data.[1]
The ANOVA tests the null hypothesis that samples in two or more groups are drawn from populations with the same mean values. To do this, two estimates are made of the population variance. These estimates rely on various assumptions (see below). The ANOVA produces an F-statistic, the ratio of the variance calculated among the means to the variance within the samples. If the group means are drawn from populations with the same mean values, the variance between the group means should be lower than the variance of the samples, following the central limit theorem. A higher ratio therefore implies that the samples were drawn from populations with different mean values.[1]
Typically, however, the one-way ANOVA is used to test for differences among at least three groups, since the two-group case can be covered by a t-test (Gosset, 1908). When there are only two means to compare, the t-test and the F-test are equivalent; the relation between ANOVA and t is given by F = t2. An extension of one-way ANOVA is two-way analysis of variance that examines the influence of two different categorical independent variables on one dependent variable.
Assumptions
The results of a one-way ANOVA can be considered reliable as long as the following assumptions are met:
- Response variable residuals are normally distributed (or approximately normally distributed).
- Samples are independent.
- Variances of populations are equal.
- Responses for a given group are independent and identically distributed normal random variables (not a simple random sample (SRS)).
ANOVA is a relatively robust procedure with respect to violations of the normality assumption.[2] If data are ordinal, a non-parametric alternative to this test should be used such as Kruskal–Wallis one-way analysis of variance.
The case of fixed effects, fully randomized experiment, unbalanced data
The model
The normal linear model describes treatment groups with probability distributions which are identically bell-shaped (normal) curves with different means. Thus fitting the models requires only the means of each treatment group and a variance calculation (an average variance within the treatment groups is used). Calculations of the means and the variance are performed as part of the hypothesis test.
The commonly used normal linear models for a completely randomized experiment are:[3]
-
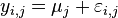 (the means model)
(the means model)
or
-
 (the effects model)
(the effects model)
where
-
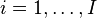 is an index over experimental units
is an index over experimental units -
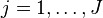 is an index over treatment groups
is an index over treatment groups -
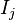 is the number of experimental units in the jth treatment group
is the number of experimental units in the jth treatment group -
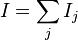 is the total number of experimental units
is the total number of experimental units -
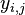 are observations
are observations -
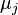 is the mean of the observations for the jth treatment group
is the mean of the observations for the jth treatment group -
 is the grand mean of the observations
is the grand mean of the observations -
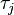 is the jth treatment effect, a deviation from the grand mean
is the jth treatment effect, a deviation from the grand mean -
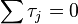
-
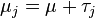
-
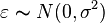 ,
, 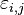 are normally distributed zero-mean random errors.
are normally distributed zero-mean random errors.
The index i over the experimental units can be interpreted several
ways. In some experiments, the same experimental unit is subject to
a range of treatments; i may point to a particular unit. In others,
each treatment group has a distinct set of experimental units; i may
simply be an index into the 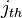 list.
list.
The data and statistical summaries of the data
One form of organizing experimental observations 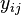 is with groups in columns:
is with groups in columns:
| Lists of Group Observations | ||||||||
|---|---|---|---|---|---|---|---|---|
| 1 | 2 |  |
 |
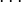 |
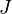 |
|||
| 1 | 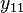 | 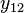 | 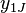 | |||||
| 2 | 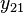 | 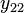 | 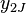 | |||||
| 3 | ||||||||
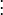 | ||||||||
 | 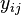 | |||||||
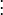 | ||||||||
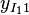 | 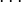 | |||||||
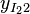 | 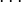 | |||||||
| Group Summary Statistics | Grand Summary Statistics | |||||||
| # Observed | 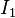 | 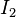 | 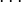 |
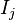 | 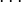 | 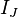 |
# Observed | 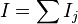 |
| Sum | 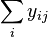 | Sum | 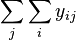 | |||||
| Sum Sq | 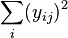 | Sum Sq | 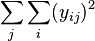 | |||||
| Mean | 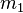 | 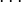 | 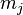 | 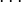 | 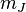 |
Mean |  | |
| Variance | 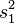 | 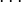 | 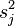 | 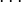 | 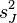 |
Variance | 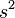 | |
Comparing model to summaries:  and
and 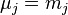 . The grand mean and grand variance are computed from the grand sums,
not from group means and variances.
. The grand mean and grand variance are computed from the grand sums,
not from group means and variances.
The hypothesis test
Given the summary statistics, the calculations of the hypothesis test are shown in tabular form. While two columns of SS are shown for their explanatory value, only one column is required to display results.
| Source of variation | Sums of squares | Sums of squares | Degrees of freedom | Mean square | F |
|---|---|---|---|---|---|
| Explanatory SS[4] | Computational SS[5] | DF | MS | ||
| Treatments | 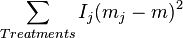 |
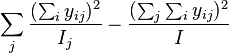 |
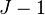 |
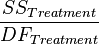 |
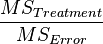 |
| Error | 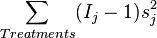 |
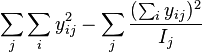 |
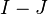 |
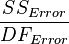 |
|
| Total | 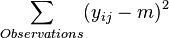 |
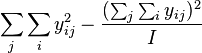 |
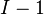 |
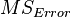 is the
estimate of variance corresponding to
is the
estimate of variance corresponding to 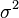 of the
model.
of the
model.
Analysis summary
The core ANOVA analysis consists of a series of calculations. The data is collected in tabular form. Then
- Each treatment group is summarized by the number of experimental units, two sums, a mean and a variance. The treatment group summaries are combined to provide totals for the number of units and the sums. The grand mean and grand variance are computed from the grand sums. The treatment and grand means are used in the model.
- The three DFs and SSs are calculated from the summaries. Then the MSs are calculated and a ratio determines F.
- A computer typically determines a p-value from F which determines whether treatments produce significantly different results. If the result is significant, then the model provisionally has validity.
If the experiment is balanced, all of the 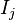 terms are
equal so the SS equations simplify.
terms are
equal so the SS equations simplify.
In a more complex experiment, where the experimental units (or
environmental effects) are not homogeneous, row statistics are also
used in the analysis. The model includes terms dependent on
 . Determining the extra terms reduces the number of
degrees of freedom available.
. Determining the extra terms reduces the number of
degrees of freedom available.
References
- George Casella (18 April 2008). Statistical design. Springer. ISBN 978-0-387-75965-4.
See also
- F test (Includes a one-way ANOVA example)
Notes
- ↑ 1.0 1.1 Howell, David (2002). Statistical Methods for Psychology. Duxbury. pp. 324–325. ISBN 0-534-37770-X.
- ↑ Kirk, RE (1995). Experimental Design: Procedures For The Behavioral Sciences (3 ed.). Pacific Grove, CA, USA: Brooks/Cole.
- ↑ Montgomery, Douglas C. (2001). Design and Analysis of Experiments (5th ed.). New York: Wiley. p. Section 3-2. ISBN 9780471316497.
- ↑ Moore, David S.; McCabe, George P. (2003). Introduction to the Practice of Statistics (4th ed.). W H Freeman & Co. p. 764. ISBN 0716796570.
- ↑ Winkler, Robert L.; Hays, William L. (1975). Statistics: Probability, Inference, and Decision (2nd ed.). New York: Holt, Rinehart and Winston. p. 761.