Odd number theorem
The odd number theorem is a theorem in strong gravitational lensing which comes directly from differential topology. It says that the number of multiple images produced by a bounded transparent lens must be odd.
In fact, the gravitational lensing is a mapping from image plane to source plane 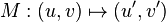 . If we use direction cosines describing the bent light rays, we can write a vector field on
. If we use direction cosines describing the bent light rays, we can write a vector field on 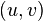 plane
plane 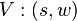 . However, only in some specific directions
. However, only in some specific directions 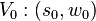 , will the bent light rays reach the observer, i.e., the images only form where
, will the bent light rays reach the observer, i.e., the images only form where 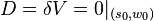 . Then we can directly apply the Poincaré–Hopf theorem
. Then we can directly apply the Poincaré–Hopf theorem 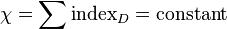 . The index of sources and sinks is +1, and that of saddle points is −1. So the Euler characteristic equals the difference between the number of positive indices
. The index of sources and sinks is +1, and that of saddle points is −1. So the Euler characteristic equals the difference between the number of positive indices 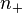 and the number of negative indices
and the number of negative indices 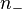 . For the far field case, there is only one image, i.e.,
. For the far field case, there is only one image, i.e.,  . So the total number of images is
. So the total number of images is 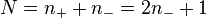 , i.e., odd. The strict proof needs Uhlenbeck’s Morse theory of null geodesics.
, i.e., odd. The strict proof needs Uhlenbeck’s Morse theory of null geodesics.
References
- Chwolson O., 1924. "Über eine mögliche Form fiktiver Doppelsterne", "Astronomische Nachrichten" 221, 329-330.
- Burke W.L., 1981. "Multiple gravitational imaging by distributed masses", Astrophysical Journal 244, L1.
- McKenzie R.H., 1985. "A gravitational lens produced an odd number of images", Journal of Mathematical Physics 26, 1592.
- Kozameh C, Lamberti P. W., Reula O. Global aspects of light cone cuts. J. Math. Phys. 32, 3423-3426 (1991).
- Lombardi M., An application of the topological degree to gravitational lenses. Modern Phys. Lett. A 13, 83-86 (1998).
- Wambsganss J., 1998. "Gravtational lensing in astronomy" http://mathnet.preprints.org/EMIS/journals/LRG/Articles/lrr-1998-12/
- Schneider P., Ehlers J., Falco E. E. 1999. "Gravitational Lenses" Astronomy and Astrophysics Library. Springer
- Giannoni F., Lombardi M, 1999. "Gravitational lenses: Odd or even images?" "Class. Quantum Grav." 16, 375-415.
- Fritelli S., Newman E. T., 1999. "Exact universal gravitational lens equations" "Phys. Rev." D 59, 124001
- Perlick V., Gravitational lensing in asymptotically simple and empty spacetimes, Annalen der Physik 9, SI139-SI142 (2000)
- Perlick V., Gravitational lensing from a geometric viewpoint, in B. Schmidt (ed.) "Einstein's field equations and their physical interpretations" Selected Essays in Honour of Jürgen Ehlers, Springer, Heidelberg (2000) pp. 373–425
- Perlick V., 2010. "Gravitational Lensing from a Spacetime Perspective" http://arxiv.org/abs/1010.3416