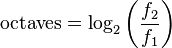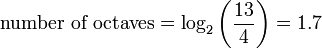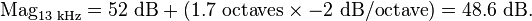Octave (electronics)

In electronics, an octave is a doubling or halving of a frequency. The term is derived from the Western musical scale (an octave is a doubling in frequency) and is therefore common in audio electronics. (The prefix octa-, denoting eight, refers to the eight notes of a diatonic scale.) Along with the decade, it is a unit used to describe frequency bands or frequency ratios.[1][2]

A frequency ratio expressed in octaves is the base-2 logarithm (binary logarithm) of the ratio:

\mathrm{octaves} = \log_2\left(\frac{f_2}{f_1}\right)

An amplifier or filter may be stated to have a frequency response of ±6dB per octave over a particular frequency range, which signifies that the power gain changes by ±6 decibels (a factor of 4 in power), when the frequency changes by a factor of 2. This slope, or more precisely 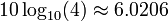10\log_{10}(4) \approx 6.0206 decibels per octave, corresponds to an amplitude gain proportional to frequency, which is equivalent to ±20dB per decade (factor of 10 amplitude gain change for a factor of 10 frequency change). This would be a first-order filter.

Example

1. The distance between the frequencies 20 Hz and 40 Hz is 1 octave.

2. An amplitude of 52 dB at 4 kHz decreases as frequency increases at −2 dB/octave. What is the amplitude at 13 kHz?

\text{number of octaves} = \log_2\left(\frac{13}{4}\right) = 1.7
\text{Mag}_{13\text{ kHz}} = 52\text{ dB} + (1.7\text{ octaves} \times -2\text{ dB/octave}) = 48.6\text{ dB}.\,

References

  1. ↑ Levine, William S. (2010). The Control Handbook: Control System Fundamentals, p.9-29. ISBN 9781420073621/ISBN 9781420073669.
  2. ↑ Perdikaris, G. (1991). Computer Controlled Systems: Theory and Applications, p.117. ISBN 9780792314226.