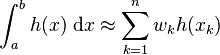Nyström method

In numerical analysis, the Nyström method[1] or quadrature method seeks the numerical solution of an integral equation by replacing the integral with a representative weighted sum. The continuous problem is broken into n discrete intervals, quadrature or numerical integration determines the weights and locations of representative points for the integral. The discrete problem to be solved is now a system of linear equations with n equations and n unknowns.

From the n solved points the function value at other points is interpolated consistent with the chosen quadrature method. Depending on the original problem and the choice of quadrature the problem may be ill-conditioned.

Since the linear equations require 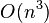O(n^3) operations to solve, hence high-order quadrature rules perform better because low-order quadrature rules require large n for a given accuracy. Gaussian quadrature is normally a good choice for smooth, non-singular problems.

Discretization of the integral

\int_a^b h (x) \;\mathrm d x \approx \sum_{k=1}^n w_k h (x_k)
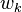where w_k are the weights of the quadrature rule, and points 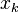x_k are the abscissas.

Example

Applying this to the inhomogeneous Fredholm equation of the second kind

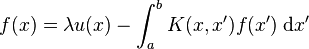f (x) = \lambda u (x) - \int_a^b K (x, x') f (x') \;\mathrm d x',

results in

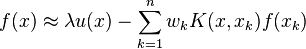f (x) \approx \lambda u (x) - \sum_{k=1}^n w_k K (x, x_k) f (x_k).

References

  1. ↑ Nyström, Evert Johannes (1930). "Über die praktische Auflösung von Integralgleichungen mit Anwendungen auf Randwertaufgaben". Acta Mathematica 54 (1): 185–204. doi:10.1007/BF02547521.