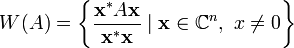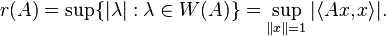Numerical range

In the mathematical field of linear algebra and convex analysis, the numerical range or field of values of a complex n × n matrix A is the set

W(A) = \left\{\frac{\mathbf{x}^*A\mathbf{x}}{\mathbf{x}^*\mathbf{x}} \mid \mathbf{x}\in\mathbb{C}^n,\ x\not=0\right\}

where x* denotes the Hermitian adjoint of the vector x.

In engineering, numerical ranges are used as a rough estimate of eigenvalues of A. Recently, generalizations of numerical range are used to study quantum computing.

A related concept is the numerical radius, which is the largest absolute values of the numbers in the numerical range, i.e.

r(A) = \sup \{ |\lambda| : \lambda \in W(A) \} = \sup_{\|x\|=1} |\langle Ax, x \rangle|.

r(A) is a norm.

Properties

The numerical range is the range of the Rayleigh quotient.
(Hausdorff–Toeplitz theorem) The numerical range is convex and compact.
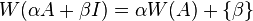$W(\alpha A+\beta I)=\alpha W(A)+\{\beta\}$ for all square matrix A and complex numbers α and β. Here I is the identity matrix.
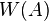$W(A)$ is a subset of the closed right half-plane if and only if 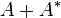$A+A^*$ is positive semidefinite.
The numerical range 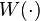$W(\cdot)$ is the only function on the set of square matrices that satisfies (2), (3) and (4).
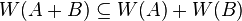(Sub-additive) $W(A+B)\subseteq W(A)+W(B)$ .
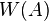$W(A)$ contains all the eigenvalues of A.
The numerical range of a 2×2 matrix is an elliptical disk.
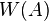$W(A)$ is a real line segment [α, β] if and only if A is a Hermitian matrix with its smallest and the largest eigenvalues being α and β
If A is a normal matrix then 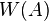$W(A)$ is the convex hull of its eigenvalues.
If α is a sharp point on the boundary of 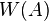$W(A)$ , then α is a normal eigenvalue of A.
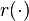$r(\cdot)$ is a norm on the space of n×n matrices.
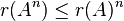
$r(A^n) \le r(A)^n$

Generalisations

C - numerical range
Higher rank numerical range
Joint numerical range
Product numerical range
Polynomial numerical hull

References

Bibliography

Choi, M.D.; Dribs, D.W.; Życzkowski (2006), "Quantum error correcting codes from the compression formalism", Rep. Math. Phys., 58, 2006 .
Dirr, G.; Helmkel, U.; Kleinsteuber, M.; Schulte-Herbrüggen, Th. (2006), "A new type of C-numerical range arising in quantum computing", Proc. Appl. Math. Mech. 6, 711–712 (2006) .
Bonsall, F.F.; Duncan, J. (1971), Numerical Ranges of Operators on Normed Spaces and of Elements of Normed Algebras, Cambridge University Press, ISBN 978-0-521-07988-4 .
Bonsall, F.F.; Duncan, J. (1971), Numerical Ranges II, Cambridge University Press, ISBN 978-0-521-20227-5 .
Horn, Roger A.; Johnson, Charles R. (1991), Topics in Matrix Analysis, Cambridge University Press, ISBN 978-0-521-46713-1 .
Li, C.K. (1996), "A simple proof of the elliptical range theorem", Proc. Am. Math. Soc. 124, 1985 .
Keeler, Dennis S.; Rodman, Leiba; Spitkovsky, Ilya M. (1997), "The numerical range of 3 × 3 matrices", Linear Algebra Applications 252, 115 .
Roger A. Horn and Charles R. Johnson, Topics in Matrix Analysis, Chapter 1, Cambridge University Press, 1991. ISBN 0-521-30587-X (hardback), ISBN 0-521-46713-6 (paperback).
"Functional Characterizations of the Field of Values and the Convex Hull of the Spectrum", Charles R. Johnson, Proceedings of the American Mathematical Society, 61(2):201-204, Dec 1976.

Numerical range

Properties

Generalisations

See also

References