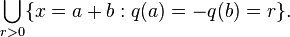Null vector

For the additive identity of a vector space, see zero element.

A null cone where n = 3

In mathematics, a null vector, or isotropic vector, is an element x of a pseudo-Euclidean space (X, q) such that q(x) = 0. Suppose $q(x) =\sum_ 1 ^ k x_i^2 - \sum_ {k+1} ^ n x_i^2 .$

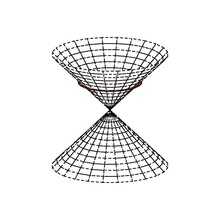
A pseudo-Euclidean space is decomposed into subspaces A and B, X = A + B, where q is positive on A and negative on B. The null cone, or isotropic cone, of X consists of the union of balanced spheres:

\bigcup_{ r>0} \{x = a + b : q(a) = - q(b) = r \}.

In the theory of bilinear forms a distinction is made between definite quadratic forms where null vectors never occur, and the other kind called isotropic quadratic forms. This context frequently refers to a null vector as an isotropic vector.

Examples

The light-like vectors of Minkowski space are null vectors.

The four linearly independent biquaternions l = 1 + hi, n = 1 + hj, m = 1 + hk, and m* = 1 – hk are null vectors and { l, n, m, m* } can serve as a basis for the subspace used to represent spacetime. Null vectors are also used in the Newman-Penrose formalism approach to spacetime manifolds.^[1]

In the Verma module of a Lie algebra there are null vectors.

References

↑ Patrick Dolan (1968) A Singularity-free solution of the Maxwell-Einstein Equations, Communications in Mathematical Physics 9(2):161-8, especially 166, link from Project Euclid

B.A. Dubrovin, A. T. Fomenko, S.P. Novikov (1984) Modern Geometry — Methods and Applications, Robert G. Burns translator, page 50, Springer ISBN 0-387-90872-2.
Ronald Shaw (1982) Linear Algebra and Group Representations, v. 1, p. 151, Academic Press ISBN 0-12-639201-3.