Notation for theoretic scheduling problems
A convenient notation for theoretic scheduling problems was introduced by Ronald Graham, Eugene Lawler, Jan Karel Lenstra and Alexander Rinnooy Kan in.[1] It consists of three fields: α, β and γ.
Each field may be a comma separated list of words. The α field describes the machine environment, β the job characteristics, and γ the objective function.
Machine environment
Single stage problems
Each job comes with a given processing time.
- 1
- there is a single machine
- P
- there are
 parallel identical machines
parallel identical machines - Q
- there are
 parallel machines with different given speeds, length of job
parallel machines with different given speeds, length of job  on machine
on machine 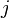 is the processing time
is the processing time 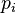 divided by speed
divided by speed 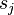
- R
- there are
 parallel unrelated machines, there are given processing times
parallel unrelated machines, there are given processing times 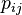 for job
for job  on machine
on machine 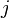
The last three letters might be followed by the number of machines which is then fixed, here  stands then for a fixed number.
stands then for a fixed number.
Multi-stage problem
- O
- open shop problem
- F
- flow shop problem
- J
- job shop problem
Job characteristics
The processing time may be equal for all jobs (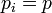 , or
, or  ) or even of unit length (
) or even of unit length (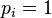 , or
, or 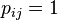 ). This makes a difference because all release times, deadlines are assumed to be integer.
). This makes a difference because all release times, deadlines are assumed to be integer.
-
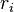
- for each job a release time is given before which it cannot be scheduled, default is 0.
-
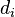
- for each job a deadline is given after which it cannot be scheduled. If the objective is
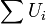 for example, then this field is implicitly assumed.
for example, then this field is implicitly assumed. - pmtn
- the jobs may be preempted and execution resumed later, possibly on a different machine
-
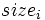
- Each job comes with a number of machines on which it must be scheduled at the same time, default is 1.
Precedence relations might be given for the jobs, in form of a partial order, meaning that if i is a predecessor of i' in that order, i' can start only when i is completed.
- prec
- an arbitrary precedence relation is given
- sp-tree, tree, intree, outtree, chain
- specific partial orders
Objective functions
Most objective functions depend on the deadline 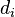 and the completion time
and the completion time 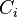 of job
of job  . We define lateness
. We define lateness 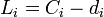 , earliness
, earliness 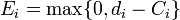 , tardiness
, tardiness 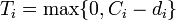 , unit penalty
, unit penalty 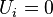 if
if 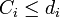 and
and 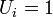 otherwise. The common objective functions are
otherwise. The common objective functions are 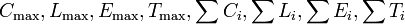 or weighted version of these sums, where every job comes with a priority
or weighted version of these sums, where every job comes with a priority 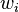 .
.
Examples
Adapted from [1]
- 1|prec|
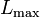
- a single machine, general precedence constraint, minimizing maximum lateness.
- R|pmtn|
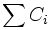
- variable number of unrelated parallel machines, allowing preemption, minimizing total completion time.
- J3|
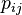 |
|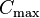
- 3-machines job shop with unit processing times, minimizing maximum completion time.
References
- B. Chen, C.N. Potts and G.J. Woeginger. "A review of machine scheduling: Complexity, algorithms and approximability". Handbook of Combinatorial Optimization (Volume 3) (Editors: D.-Z. Du and P. Pardalos), 1998, Kluwer Academic Publishers. 21-169. ISBN 0-7923-5285-8 (HB) 0-7923-5019-7 (Set)
- Peter Brucker, Sigrid Knust. Complexity results for scheduling problems
- ↑ 1.0 1.1 Graham, R. L.; Lawler, E. L.; Lenstra, J.K.; Rinnooy Kan, A.H.G. (1979). "Optimization and Approximation in Deterministic Sequencing and Scheduling: a Survey". Proceedings of the Advanced Research Institute on Discrete Optimization and Systems Applications of the Systems Science Panel of NATO and of the Discrete Optimization Symposium. Elsevier. pp. (5) 287–326.