Nonlinear expectation

In probability theory, a nonlinear expectation is a nonlinear generalization of the expectation. Nonlinear expectations are useful in utility theory as they more closely match human behavior than traditional expectations.

Definition

A functional 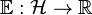$\mathbb{E}: \mathcal{H} \to \mathbb{R}$ (where 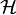$\mathcal{H}$ is a vector lattice on a probability space) is a nonlinear expectation if it satisfies:^[1]^[2]

Monotonicity: if 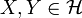$X,Y \in \mathcal{H}$ such that 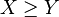$X \geq Y$ then $\mathbb{E}[X] \geq \mathbb{E}[Y]$
Preserving of constants: if 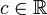$c \in \mathbb{R}$ then $\mathbb{E}[c] = c$

Often other properties are also desirable, for instance convexity, subadditivity, positive homogeneity, and translative of constants.^[1]

Examples

Expected value
Choquet expectation
g-expectation
If 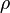$\rho$ is a risk measure then $\mathbb{E}[X] := \rho(-X)$ defines a nonlinear expectation

References

↑ 1.0 1.1 Shige Peng (2006). "G–Expectation, G–Brownian Motion and Related Stochastic Calculus of Itô Type" (pdf). Abel Symposia (Springer-Verlag) 2. Retrieved August 9, 2012.
↑ Peng, S. (2004). "Nonlinear Expectations, Nonlinear Evaluations and Risk Measures". Stochastic Methods in Finance (pdf). Lecture Notes in Mathematics 1856. pp. 165–138. doi:10.1007/978-3-540-44644-6_4. ISBN 978-3-540-22953-7. Retrieved August 9, 2012.