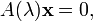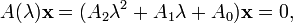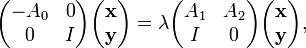Nonlinear eigenproblem
A nonlinear eigenproblem is a generalization of an ordinary eigenproblem to equations that depend nonlinearly on the eigenvalue. Specifically, it refers to equations of the form:
where x is a vector (the nonlinear "eigenvector") and A is a matrix-valued function of the number  (the nonlinear "eigenvalue"). (More generally,
(the nonlinear "eigenvalue"). (More generally, 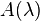 could be a linear map, but most commonly it is a finite-dimensional, usually square, matrix.) A is usually required to be a holomorphic function of
could be a linear map, but most commonly it is a finite-dimensional, usually square, matrix.) A is usually required to be a holomorphic function of  (in some domain).
(in some domain).
For example, an ordinary linear eigenproblem 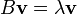 , where B is a square matrix, corresponds to
, where B is a square matrix, corresponds to 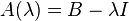 , where I is the identity matrix.
, where I is the identity matrix.
One common case is where A is a polynomial matrix, which is called a polynomial eigenvalue problem. In particular, the specific case where the polynomial has degree two is called a quadratic eigenvalue problem, and can be written in the form:
in terms of the constant square matrices A0,1,2. This can be converted into an ordinary linear generalized eigenproblem of twice the size by defining a new vector 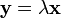 . In terms of x and y, the quadratic eigenvalue problem becomes:
. In terms of x and y, the quadratic eigenvalue problem becomes:
where I is the identity matrix. More generally, if A is a matrix polynomial of degree d, then one can convert the nonlinear eigenproblem into a linear (generalized) eigenproblem of d times the size.
Besides converting them to ordinary eigenproblems, which only works if A is polynomial, there are other methods of solving nonlinear eigenproblems based on the Jacobi-Davidson algorithm or based on Newton's method (related to inverse iteration).
References
- Françoise Tisseur and Karl Meerbergen, "The quadratic eigenvalue problem," SIAM Review 43 (2), 235-286 (2001).
- Gene H. Golub and Henk A. van der Vorst, "Eigenvalue computation in the 20th century," Journal of Computational and Applied Mathematics 123, 35-65 (2000).
- Philippe Guillaume, "Nonlinear eigenproblems," SIAM J. Matrix. Anal. Appl. 20 (3), 575-595 (1999).
- Axel Ruhe, "Algorithms for the nonlinear eigenvalue problem," SIAM Journal on Numerical Analysis 10 (4), 674-689 (1973).