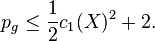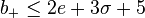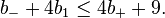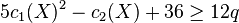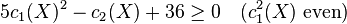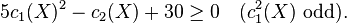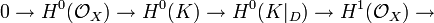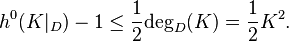Noether inequality

In mathematics, the Noether inequality, named after Max Noether, is a property of compact minimal complex surfaces that restricts the topological type of the underlying topological 4-manifold. It holds more generally for minimal projective surfaces of general type over an algebraically closed field.

Formulation of the inequality

Let X be a smooth minimal projective surface of general type defined over an algebraically closed field (or a smooth minimal compact complex surface of general type) with canonical divisor K = −c₁(X), and let p_g = h⁰(K) be the dimension of the space of holomorphic two forms, then

p_g \le \frac{1}{2} c_1(X)^2 + 2.

For complex surfaces, an alternative formulation expresses this inequality in terms of topological invariants of the underlying real oriented four manifold. Since a surface of general type is a Kähler surface, the dimension of the maximal positive subspace in intersection form on the second cohomology is given by b₊ = 1 + 2p_g. Moreover by the Hirzebruch signature theorem c₁² (X) = 2e + 3σ, where e = c₂(X) is the topological Euler characteristic and σ = b₊ − b₋ is the signature of the intersection form. Therefore the Noether inequality can also be expressed as

b_+ \le 2 e + 3 \sigma + 5 \,

or equivalently using e = 2 – 2 b₁ + b₊ + b_-

b_- + 4 b_1 \le 4b_+ + 9. \,

Combining the Noether inequality with the Noether formula 12χ=c₁²+c₂ gives

5 c_1(X)^2 - c_2(X) + 36 \ge 12q

where q is the irregularity of a surface, which leads to a slightly weaker inequality, which is also often called the Noether inequality:

5 c_1(X)^2 - c_2(X) + 36 \ge 0 \quad (c_1^2(X)\text{ even})

5 c_1(X)^2 - c_2(X) + 30 \ge 0 \quad (c_1^2(X)\text{ odd}).

Surfaces where equality holds (i.e. on the Noether line) are called Horikawa surfaces.

Proof sketch

It follows from the minimal general type condition that K² > 0. We may thus assume that p_g > 1, since the inequality is otherwise automatic. In particular, we may assume there is an effective divisor D representing K. We then have an exact sequence

0 \to H^0(\mathcal{O}_X) \to H^0(K) \to H^0( K|_D) \to H^1(\mathcal{O}_X) \to

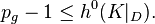
so $p_g - 1 \le h^0(K|_D).$

Assume that D is smooth. By the adjunction formula D has a canonical linebundle 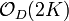$\mathcal{O}_D(2K)$ , therefore 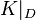$K|_D$ is a special divisor and the Clifford inequality applies, which gives

h^0(K|_D) - 1 \le \frac{1}{2}\mathrm{deg}_D(K) = \frac{1}{2}K^2.\,

In general, essentially the same argument applies using a more general version of the Clifford inequality for local complete intersections with a dualising line bundle and 1-dimensional sections in the trivial line bundle. These conditions are satisfied for the curve D by the adjunction formula and the fact that D is numerically connected.

References

Barth, Wolf P.; Hulek, Klaus; Peters, Chris A.M.; Van de Ven, Antonius (2004), Compact Complex Surfaces, Ergebnisse der Mathematik und ihrer Grenzgebiete. 3. Folge. 4, Springer-Verlag, Berlin, ISBN 978-3-540-00832-3, MR 2030225
Liedtke, Christian (2008), "Algebraic Surfaces of general type with small c₁² in positive characteristic", Nagoya Math. J. 191: 111–134
Noether, Max (1875), "Zur Theorie der eindeutigen Entsprechungen algebraischer Gebilde", Math. Ann. 8 (4): 495–533, doi:10.1007/BF02106598