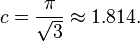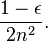No-three-in-line problem
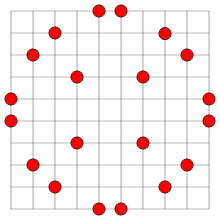
In mathematics, in the area of discrete geometry, the no-three-in-line-problem, introduced by Henry Dudeney in 1917, asks for the maximum number of points that can be placed in the n × n grid so that no three points are collinear. This number is at most 2n, since if 2n + 1 points are placed in the grid, then by the pigeonhole principle some row and some column will contain three points.
Lower bounds
Paul Erdős (in Roth 1951) observed that, when n is a prime number, the set of n grid points (i, i2 mod n), for 0 ≤ i < n, contains no three collinear points. When n is not prime, one can perform this construction for a p × p grid contained in the n × n grid, where p is the largest prime that is at most n. As a consequence, for any ε and any sufficiently large n, one can place
points in the n × n grid with no three points collinear.
Erdős' bound has been improved subsequently: Hall et al. (1975) show that, when n/2 is prime, one can obtain a solution with 3(n - 2)/2 points by placing points on the hyperbola xy ≡ k (mod n/2) for a suitable k. Again, for arbitrary n one can perform this construction for a prime near n/2 to obtain a solution with
points.
Conjectured upper bounds
Guy & Kelly (1968) conjectured that for large n one cannot do better than c n with
Pegg, Jr. (2005) noted that Gabor Ellmann found, in March 2004, an error in the original paper of Guy and Kelly's heuristic reasoning, which if corrected, results in
Applications
The Heilbronn triangle problem asks for the placement of n points in a unit square that maximizes the area of the smallest triangle formed by three of the points. By applying Erdős' construction of a set of grid points with no three collinear points, one can find a placement in which the smallest triangle has area
Generalizations
A noncollinear placement of n points can also be interpreted as a graph drawing of the complete graph in such a way that, although edges cross, no edge passes through a vertex. Erdős' construction above can be generalized to show that every n-vertex k-colorable graph has such a drawing in a O(n) × O(k) grid (Wood (2005)).
Non-collinear sets of points in the three-dimensional grid were considered by Pór & Wood (2007). They proved that the maximum number of points in the n × n × n grid with no three points collinear is 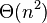 .
Similarly to Erdős's 2D construction, this can be accomplished by using points
(x, y, x2 + y2) mod p, where p is a prime congruent to 3 mod 4.
One can also consider graph drawings in the three-dimensional grid. Here the non-collinearity condition means that a vertex should not lie on a non-adjacent edge, but it is normal to work with the stronger requirement that no two edges cross (Pach, Thiele & Tóth (1998); Dujmović, Morin & Wood (2005); Di Giacomo, Liotta & Meijer (2005)).
.
Similarly to Erdős's 2D construction, this can be accomplished by using points
(x, y, x2 + y2) mod p, where p is a prime congruent to 3 mod 4.
One can also consider graph drawings in the three-dimensional grid. Here the non-collinearity condition means that a vertex should not lie on a non-adjacent edge, but it is normal to work with the stronger requirement that no two edges cross (Pach, Thiele & Tóth (1998); Dujmović, Morin & Wood (2005); Di Giacomo, Liotta & Meijer (2005)).
Small values of n
For n ≤ 46, it is known that 2n points may be placed with no three in a line. The numbers of solutions (not counting reflections and rotations as distinct) for small n = 2, 3, ..., are
References
- Dudeney, Henry (1917), Amusements in Mathematics, Edinburgh: Nelson
- Di Giacomo, Emilio; Liotta, Giuseppe; Meijer, Henk (2005), "Computing Straight-line 3D Grid Drawings of Graphs in Linear Volume", Computational Geometry: Theory and Applications 32 (1): 26–58, doi:10.1016/j.comgeo.2004.11.003
- Dujmović, Vida; Morin, Pat; Wood, David R. (2005), "Layout of Graphs with Bounded Tree-Width", SIAM Journal on Computing 34 (3): 553–579, doi:10.1137/S0097539702416141
- Felsner, Stefan; Liotta, Giuseppe; Wismath, Stephen K. (2003). "Straight-Line Drawings on Restricted Integer Grids in Two and Three Dimensions". Journal of Graph Algorithms and Applications 7 (4): 363–398. doi:10.7155/jgaa.00075.
- Flammenkamp, Achim (1992). "Progress in the no-three-in-line problem". Journal of Combinatorial Theory. Series A 60 (2): 305–311. doi:10.1016/0097-3165(92)90012-J.
- Flammenkamp, Achim (1998). "Progress in the no-three-in-line problem, II". Journal of Combinatorial Theory. Series A 81 (1): 108–113. doi:10.1006/jcta.1997.2829.
- Guy, R. K.; Kelly, P. A. (1968). "The no-three-in-line problem". Canadian Mathematical Bulletin 11 (0): 527–531. doi:10.4153/CMB-1968-062-3. MR 0238765.
- Hall, R. R.; Jackson, T. H.; Sudbery, A.; Wild, K. (1975). "Some advances in the no-three-in-line problem". Journal of Combinatorial Theory. Series A 18 (3): 336–341. doi:10.1016/0097-3165(75)90043-6.
- Lefmann, Hanno (2008). "No l Grid-Points in spaces of small dimension". Algorithmic Aspects in Information and Management, 4th International Conference, AAIM 2008, Shanghai, China, June 23-25, 2008, Proceedings. Lecture Notes in Computer Science 5034. Springer-Verlag. pp. 259–270. doi:10.1007/978-3-540-68880-8_25.
- Pach, János; Thiele, Torsten; Tóth, Géza (1998). "Three-dimensional grid drawings of graphs". Graph Drawing, 5th Int. Symp., GD '97. Lecture Notes in Computer Science 1353. Springer-Verlag. pp. 47–51. doi:10.1007/3-540-63938-1_49.
- Pegg, Jr., Ed (April 11, 2005). "Math Games: Chessboard Tasks". Retrieved June 25, 2012.
- Pór, Attila; Wood, David R. (2007). "No-three-in-line-in-3D". Algorithmica 47 (4): 481. doi:10.1007/s00453-006-0158-9.
- Roth, K. F. (1951), "On a problem of Heilbronn", Journal of the London Mathematical Society 26 (3): 198–204, doi:10.1112/jlms/s1-26.3.198
- Wood, David R. (2005). "Grid drawings of k-colourable graphs". Computational Geometry: Theory and Applications 30 (1): 25–28. doi:10.1016/j.comgeo.2004.06.001.
External links
- Flammenkamp, Achim. "The No-Three-in-Line Problem".
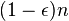
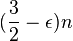
![c = \sqrt[3]{\frac{2\pi^2}{3}} \approx 1.874.](../I/m/5bed35f95a0f0024a523fdf8a325fe9e.png)