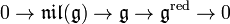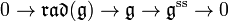Nilradical of a Lie algebra

In algebra, the nilradical of a Lie algebra is a nilpotent ideal, which is as large as possible.

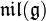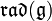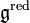The nilradical $\mathfrak{nil}(\mathfrak g)$ of a finite-dimensional Lie algebra $\mathfrak{g}$ is its maximal nilpotent ideal, which exists because the sum of any two nilpotent ideals is nilpotent. It is an ideal in the radical $\mathfrak{rad}(\mathfrak{g})$ of the Lie algebra $\mathfrak{g}$ . The quotient of a Lie algebra by its nilradical is a reductive Lie algebra $\mathfrak{g}^{\mathrm{red}}$ . However, the corresponding short exact sequence

0 \to \mathfrak{nil}(\mathfrak g)\to \mathfrak g\to \mathfrak{g}^{\mathrm{red}}\to 0

does not split in general (i.e., there isn't always a subalgebra complementary to 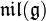$\mathfrak{nil}(\mathfrak g)$ in $\mathfrak{g}$ ). This is in contrast to the Levi decomposition: the short exact sequence

0 \to \mathfrak{rad}(\mathfrak g)\to \mathfrak g\to \mathfrak{g}^{\mathrm{ss}}\to 0

does split (essentially because the quotient 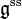$\mathfrak{g}^{\mathrm{ss}}$ is semisimple).

References

Fulton, William; Harris, Joe (1991), Representation theory. A first course, Graduate Texts in Mathematics, Readings in Mathematics 129, New York: Springer-Verlag, ISBN 978-0-387-97495-8, MR 1153249, ISBN 978-0-387-97527-6
Onishchik, Arkadi L.; Vinberg, Ėrnest Borisovich (1994), Lie Groups and Lie Algebras III: Structure of Lie Groups and Lie Algebras, Springer, ISBN 978-3-540-54683-2 .

Nilradical of a Lie algebra

See also

References