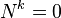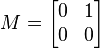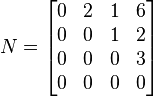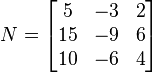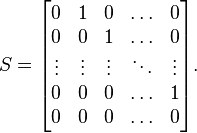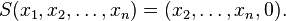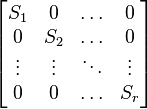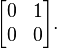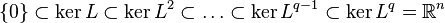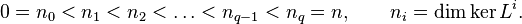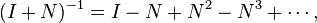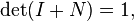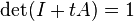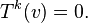Nilpotent matrix

In linear algebra, a nilpotent matrix is a square matrix N such that

N^k = 0\,

for some positive integer k. The smallest such k is sometimes called the degree of N.

More generally, a nilpotent transformation is a linear transformation L of a vector space such that L^k = 0 for some positive integer k (and thus, L^j = 0 for all j ≥ k). Both of these concepts are special cases of a more general concept of nilpotence that applies to elements of rings.

Examples

The matrix

M = \begin{bmatrix} 0 & 1 \\ 0 & 0 \end{bmatrix}

is nilpotent, since M² = 0. More generally, any triangular matrix with 0s along the main diagonal is nilpotent. For example, the matrix

N = \begin{bmatrix} 0 & 2 & 1 & 6\\ 0 & 0 & 1 & 2\\ 0 & 0 & 0 & 3\\ 0 & 0 & 0 & 0 \end{bmatrix}

is nilpotent, with

N^2 = \begin{bmatrix} 0 & 0 & 2 & 7\\ 0 & 0 & 0 & 3\\ 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 \end{bmatrix} ;\ N^3 = \begin{bmatrix} 0 & 0 & 0 & 6\\ 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 \end{bmatrix} ;\ N^4 = \begin{bmatrix} 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 \end{bmatrix}.

Though the examples above have a large number of zero entries, a typical nilpotent matrix does not. For example, the matrix

N = \begin{bmatrix} 5 & -3 & 2 \\ 15 & -9 & 6 \\ 10 & -6 & 4 \end{bmatrix}

squares to zero, though the matrix has no zero entries.

Characterization

For an n × n square matrix N with real (or complex) entries, the following are equivalent:

N is nilpotent.
The minimal polynomial for N is λ^k for some positive integer k ≤ n.
The characteristic polynomial for N is λⁿ.
The only eigenvalue for N is 0.
tr(N^k) = 0 for all k > 0.

The last theorem holds true for matrices over any field of characteristic 0 or sufficiently large characteristic. (cf. Newton's identities)

This theorem has several consequences, including:

The degree of an n × n nilpotent matrix is always less than or equal to n. For example, every 2 × 2 nilpotent matrix squares to zero.
The determinant and trace of a nilpotent matrix are always zero.
The only nilpotent diagonalizable matrix is the zero matrix.

Classification

Consider the n × n shift matrix:

S = \begin{bmatrix} 0 & 1 & 0 & \ldots & 0 \\ 0 & 0 & 1 & \ldots & 0 \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & 0 & \ldots & 1 \\ 0 & 0 & 0 & \ldots & 0 \end{bmatrix}.

This matrix has 1s along the superdiagonal and 0s everywhere else. As a linear transformation, the shift matrix “shifts” the components of a vector one slot to the left:

S(x_1,x_2,\ldots,x_n) = (x_2,\ldots,x_n,0).

This matrix is nilpotent with degree n, and is the “canonical” nilpotent matrix.

Specifically, if N is any nilpotent matrix, then N is similar to a block diagonal matrix of the form

\begin{bmatrix} S_1 & 0 & \ldots & 0 \\ 0 & S_2 & \ldots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \ldots & S_r \end{bmatrix}

where each of the blocks S₁, S₂, ..., S_r is a shift matrix (possibly of different sizes). This theorem is a special case of the Jordan canonical form for matrices.

For example, any nonzero 2 × 2 nilpotent matrix is similar to the matrix

\begin{bmatrix} 0 & 1 \\ 0 & 0 \end{bmatrix}.

That is, if N is any nonzero 2 × 2 nilpotent matrix, then there exists a basis b₁, b₂ such that Nb₁ = 0 and Nb₂ = b₁.

This classification theorem holds for matrices over any field. (It is not necessary for the field to be algebraically closed.)

Flag of subspaces

A nilpotent transformation L on Rⁿ naturally determines a flag of subspaces

\{0\} \subset \ker L \subset \ker L^2 \subset \ldots \subset \ker L^{q-1} \subset \ker L^q = \mathbb{R}^n

and a signature

0 = n_0 < n_1 < n_2 < \ldots < n_{q-1} < n_q = n,\qquad n_i = \dim \ker L^i.

The signature characterizes L up to an invertible linear transformation. Furthermore, it satisfies the inequalities

n_{j+1} - n_j \leq n_j - n_{j-1}, \qquad \mbox{for all } j = 1,\ldots,q-1.

Conversely, any sequence of natural numbers satisfying these inequalities is the signature of a nilpotent transformation.

Additional properties

If N is nilpotent, then I + N is invertible, where I is the n × n identity matrix. The inverse is given by

(I + N)^{-1} = I - N + N^2 - N^3 + \cdots,

where only finitely many terms of this sum are nonzero.

If N is nilpotent, then

\det (I + N) = 1,\!\,

where I denotes the n × n identity matrix. Conversely, if A is a matrix and

\det (I + tA) = 1\!\,

for all values of t, then A is nilpotent. In fact, since

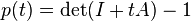p(t) = \det (I + tA) - 1

is a polynomial of degree

n

, it suffices to have this hold for

n+1

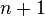distinct values of

t

Every singular matrix can be written as a product of nilpotent matrices.^[1]

Generalizations

A linear operator T is locally nilpotent if for every vector v, there exists a k such that

T^k(v) = 0.\!\,

For operators on a finite-dimensional vector space, local nilpotence is equivalent to nilpotence.

References

↑ R. Sullivan, Products of nilpotent matrices, Linear and Multilinear Algebra, Vol. 56, No. 3

External links

Nilpotent matrix and nilpotent transformation on PlanetMath.