Nilpotent algebra (ring theory)

In mathematics, specifically in ring theory, a nilpotent algebra over a commutative ring is an algebra over a commutative ring, in which for some positive integer n every product containing at least n elements of the algebra is zero. The concept of a nilpotent Lie algebra has a different definition, which depends upon the Lie bracket. (There is no Lie bracket for many algebras over commutative rings; a Lie algebra involves its Lie bracket, whereas, there is no Lie bracket defined in the general case of an algebra over a commutative ring.) Another possible source of confusion in terminology is the quantum nilpotent algebra,[1] a concept related to quantum groups and Hopf algebras.

Formal definition

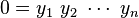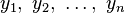An associative algebra A over a commutative ring R is defined to be a nilpotent algebra if and only if there exists some positive integer n such that 0=y_1\ y_2\ \cdots\ y_n for all y_1, \ y_2, \ \ldots,\ y_n in the algebra A. The smallest such n is called the index of the algebra A.[2] In the case of a non-associative algebra, the definition is that every different multiplicative association of the n elements is zero.

Nil algebra

An algebra in which every element of the algebra is nilpotent is called a nil algebra.[3]

See also

References

  1. ↑ Goodearl, K. R.; Yakimov, M. T. (1 Nov 2013). "Unipotent and Nakayama automorphisms of quantum nilpotent algebras". arxiv.org.
  2. ↑ Albert, A. Adrian (2003) [1939]. "Chapt. 2: Ideals and Nilpotent Algebras". Structure of Algebras. Colloquium Publications, Col. 24. Amer. Math. Soc. p. 22. ISBN 0-8218-1024-3. ISSN 0065-9258; reprint with corrections of revised 1961 edition
  3. ↑ Nil algebra – Encyclopedia of Mathematics

External links