Nicole Oresme
| Nicole Oresme | |
|---|---|
 | |
| Born |
1323 Fleury-sur-Orne, Normandy, France |
| Died |
11 July 1382 Lisieux, Normandy, France |
| Era | 14th-century philosophy |
| Region | Western Philosophy |
Main interests | Natural philosopher, astronomy, theology, mathematical |
|
Influences
| |
Nicole Oresme (French: [nikɔl ɔʁɛm];[1] c. 1320–1325 – July 11, 1382), also known as Nicolas Oresme, Nicholas Oresme, or Nicolas d'Oresme, was a significant philosopher of the later Middle Ages. He wrote influential works on economics, mathematics, physics, astrology and astronomy, philosophy, and theology; was Bishop of Lisieux, a translator, a counselor of King Charles V of France, and probably one of the most original thinkers of the 14th century.[2]
Oresme's life
Nicole Oresme was born c. 1320-1325 in the village of Allemagne (today's Fleury-sur-Orne) in the vicinity of Caen, Normandy, in the diocese of Bayeux. Practically nothing is known concerning his family. The fact that Oresme attended the royally sponsored and subsidized College of Navarre, an institution for students too poor to pay their expenses while studying at the University of Paris, makes it probable that he came from a peasant family.[3]
Oresme studied the "artes" in Paris, together with Jean Buridan (the so-called founder of the French school of natural philosophy), Albert of Saxony and perhaps Marsilius of Inghen, and there received the Magister Artium. He was already a regent master in arts by 1342, during the crisis over William of Ockham's natural philosophy.[4]
In 1348, he was a student of theology in Paris. In 1356, he received his doctorate and in the same year he became grand master (grand-maître) of the College of Navarre. In 1364, he was appointed dean of the Cathedral of Rouen. Around 1369, he began a series of translations of Aristotelian works at the request of Charles V, who granted him a pension in 1371 and, with royal support, was appointed bishop of Lisieux in 1377. In 1382, he died in Lisieux.[5]
Oresme's scientific work
Cosmology

In his Livre du ciel et du monde Oresme discussed a range of evidence for and against the daily rotation of the Earth on its axis.[6] From astronomical considerations, he maintained that if the Earth were moving and not the celestial spheres, all the movements that we see in the heavens that are computed by the astronomers would appear exactly the same as if the spheres were rotating around the Earth. He rejected the physical argument that if the Earth were moving the air would be left behind causing a great wind from east to west. In his view the Earth, Water, and Air would all share the same motion.[7] As to the scriptural passage that speaks of the motion of the Sun, he concludes that "this passage conforms to the customary usage of popular speech" and is not to be taken literally.[8] He also noted that it would be more economical for the small Earth to rotate on its axis than the immense sphere of the stars.[9] Nonetheless, he concluded that none of these arguments were conclusive and "everyone maintains, and I think myself, that the heavens do move and not the Earth."[10]
Critiques of astrology
In his mathematical work, Oresme developed the notion of incommensurate fractions, fractions that could not be expressed as powers of one another, and made probabilistic, statistical arguments as to their relative frequency.[11] From this, he argued that it was very probable that the length of the day and the year were incommensurate (irrational), as indeed were the periods of the motions of the moon and the planets. From this, he noted that planetary conjunctions and oppositions would never recur in quite exactly the same way. Oresme maintained that this disproves the claims of astrologers who, thinking "they know with punctual exactness the motions, aspects, conjunctions and oppositions… [judge] rashly and erroneously about future events."[12]
Oresme's critique of astrology in his Livre de divinacions treats it as having six parts.[13] The first, essentially astronomy, the movements of heavenly bodies, he considers good science but not precisely knowable. The second part deals with the influences of the heavenly bodies on earthly events at all scales. Oresme does not deny such influence, but states, in line with a commonly held opinion,[14] that it could either be that arrangements of heavenly bodies signify events, purely symbolically, or that they actually cause such events, deterministically. Mediaevalist Chauncey Wood remarks that this major elision "makes it very difficult to determine who believed what about astrology."[14] The third part concerns predictiveness, covering events at three different scales: great events such as plagues, famines, floods and wars; weather, winds and storms; and medicine, with influences on the humours, the four Aristotelian fluids of the body. Oresme criticizes all of these as misdirected, though he accepts that prediction is a legitimate area of study, and argues that the effect on the weather is less well known than the effect on great events. He observes that sailors and farmers are better at predicting weather than astrologers, and specifically attacks the astrological basis of prediction, noting correctly that the zodiac has moved relative to the fixed stars (because of precession of the equinoxes) since the zodiac was first described in ancient times.[14] These first three parts are what Oresme considers the physical influences of the stars and planets (including sun and moon) on the earth, and while he offers critiques of them, he accepts that effects exist. The last three parts are what Oresme considers to concern (good or bad) fortune. They are interrogations, meaning asking the stars when to do things such as business deals; elections, meaning choosing the best time to do things such as getting married or fighting a war; and nativities, meaning the natal astrology with birth charts that forms much of modern astrological practice. Oresme classifies interrogations and elections as "totally false" arts, but his critique of nativities is more measured. He denies that any path is predetermined by the heavenly bodies, because humans have free will, but he accepts that the heavenly bodies can influence behaviour and habitual mood, via the combination of humours in each person. Overall, Oresme's skepticism is strongly shaped by his understanding of the scope of astrology. He accepts things a modern skeptic would reject, and rejects some things — such as the knowability of planetary movements, and effects on weather — that are accepted by modern science.[15]
Sense perception
In discussing the propagation of light and sound, Oresme adopted the common medieval doctrine of the multiplication of species,[16] as it had been developed by optical writers such as Alhacen, Robert Grosseteste, Roger Bacon, John Pecham, and Witelo.[17] Oresme maintained that these species were immaterial, but corporeal (i.e., three-dimensional), entities.[18]
Translations
Like most of his scholarly contemporaries, Oresme wrote primarily in Latin, but at the urging of King Charles V, he also wrote in French, providing French versions of his own works and of selected works by Aristotle.
Mathematics
Oresme's most important contributions to mathematics are contained in Tractatus de configurationibus qualitatum et motuum. In a quality, or accidental form, such as heat, he distinguished the intensio (the degree of heat at each point) and the extensio (as the length of the heated rod). These two terms were often replaced by latitudo and longitudo. For the sake of clarity, Oresme conceived the idea of visualizing these concepts by plane figures, approaching what we would now call rectangular co-ordinates. The intensity of the quality was represented by a length or latitudo proportional to the intensity erected perpendicular to the base at a given point on the base line, which represents the longitudo. Oresme proposed that the geometrical form of such a figure could be regarded as corresponding to a characteristic of the quality itself. Oresme defined a uniform quality as that which is represented by a line parallel to the longitude, and any other quality as difform. Uniformly varying qualities are represented by a straight line inclined to the axis of the longitude, while he described many cases of nonuniformly varying qualities. Oresme extended this doctrine to figures of three dimensions. He considered this analysis applicable to many different qualities such as hotness, whiteness, and sweetness. Significantly for later developments, Oresme applied this concept to the analysis of local motion where the latitudo or intensity represented the speed, the longitudo represented the time, and the area of the figure represented the distance travelled.[19]
He shows that his method of figuring the latitude of forms is applicable to the movement of a point, on condition that the time is taken as longitude and the speed as latitude; quantity is, then, the space covered in a given time. In virtue of this transposition, the theorem of the latitudo uniformiter difformis became the law of the space traversed in case of uniformly varied motion; thus Oresme published what was taught over two centuries prior to Galileo´s making it famous.[20][21]
Significantly, Oresme developed the first proof of the divergence of the harmonic series, something that was only replicated in later centuries by the Bernoulli brothers. His proof, requiring less advanced mathematics than current "standard" tests for divergence (for example, the integral test), begins by noting that for any n that is a power of 2, there are n/2 terms in the series between 1/(n/2) and 1/n. Each of these terms is at least 1/n, and since there are n/2 of them they sum to at least 1/2. For instance, there is one term 1/2, then two terms 1/3+1/4 that together sum to at least 1/2, then four terms 1/5+1/6+1/7+1/8 that also sum to at least 1/2, and so on. Thus the series must be greater than the series 1 + 1/2 + 1/2 + 1/2 + ... + 1/2, which does not have a finite limit. This proves that the harmonic series must be divergent. This argument shows that the sum of the first n terms grows as 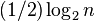 , which is correct within a multiplicative constant.
, which is correct within a multiplicative constant.
Oresme was the first mathematician to prove this fact, and (after his proof was lost) it was not proven again until the 17th century by Pietro Mengoli.[22]
He also worked on fractional powers, and the notion of probability over infinite sequences, ideas which would not be further developed for the next three and five centuries, respectively.[11]
Economics
With his Treatise on the origin, nature, law, and alterations of money (De origine, natura, jure et mutationibus monetarum), one of the earliest manuscripts devoted to an economic matter, Oresme brings an interesting insight on the medieval conception of money.
Translations
- Nicole Oresme's De visione stellarum (On seeing the stars): a critical edition of Oresme's treatise on optics and atmospheric refraction, translated by Dan Burton, (Leiden; Boston: Brill, 2007)
- Nicole Oresme and The marvels of nature: a study of his De causis mirabilium, translated by Bert Hansen, (Toronto: Pontifical Institute of Mediaeval Studies, 1985)
- Questiones super quatuor libros meteororum, in SC McCluskey, ed, Nicole Oresme on Light, Color and the Rainbow: An Edition and Translation, with introduction and critical notes, of Part of Book Three of his Questiones super quatuor libros meteororum , (PhD dissertation, University of Wisconsin, 1974)
- Nicole Oresme and the kinematics of circular motion: Tractatus de commensurabilitate vel incommensurabilitate motuum celi, translated by Edward Grant, (Madison: University of Wisconsin Press, 1971)
- Nicole Oresme and the medieval geometry of qualities and motions: a treatise on the uniformity and difformity of intensities known as Tractatus de configurationibus qualitatum et motuum, translated by Marshall Clagett, (Madison: University of Wisconsin Press, 1968)
- Le Livre du ciel et du monde. A. D. Menut and A. J. Denomy, ed. Madison: University of Wisconsin Press, 1968.
- De proportionibus proportionum and Ad pauca respicientes. Edward Grant, ed. and trans. Madison: University of Wisconsin Press, 1966.
- The De moneta of N. Oresme, and English Mint documents, translated by C. Johnson, (London, 1956)
See also
- List of multiple discoveries
- Science in the Middle Ages
- Oresme (crater)
- List of Roman Catholic scientist-clerics
Footnotes
- ↑ Léon Warnant (1987). Dictionnaire de la prononciation française dans sa norme actuelle (in French) (3rd ed.). Gembloux: J. Duculot, S. A. ISBN 978-2-8011-0581-8.
- ↑ Wallace, William A. (1981). Prelude to Galileo: essays on medieval and sixteenth-century sources of Galileo's thought. Springer Science & Business. ISBN 978-9027712158.
- ↑ Edward Grant, ed., De proportionibus proportionum and Ad pauca respicientes, (Madison: University of Wisconsin Pr., 1966), p. 4.
- ↑ William J. Courtenay, The Early Career of Nicole Oresme, Isis, Vol. 91, No.3 (Sept., 2000), pp 542–548.
- ↑ Edward Grant, ed., De proportionibus proportionum and Ad pauca respicientes, (Madison: University of Wisconsin Pr., 1966), pp. 4–10.
- ↑ Edward Grant, The Foundations of Modern Science in the Middle Ages, (Cambridge: Cambridge University Press, 1996), pp. 114–16.
- ↑ Oresme, Le Livre du ciel et du monde, pp. 521–3
- ↑ Oresme, Le Livre du ciel et du monde, p. 531
- ↑ Oresme, Le Livre du ciel et du monde, p. 535
- ↑ Oresme, Le Livre du ciel et du monde, p. 537
- ↑ 11.0 11.1 James Franklin, The Science of Conjecture, Evidence and Probability before Pascal (Johns Hopkins University Press, 2001), ISBN 0-8018-7109-3 (see chapter 6, pp.140 - 145)
- ↑ Oresme, Ad pauca respicientes, p. 383.
- ↑ Coopland, G. W. (1952). Nicole Oresme and the Astrologers: A Study of his Livre de Divinacions. Harvard University Press; Liverpool University Press. pp. 53–57.
- ↑ 14.0 14.1 14.2 Wood, 1970. p. 9
- ↑ Wood, 1970. pp. 8–11
- ↑ Bert Hansen, Nicole Oresme and the Marvels of Nature (Toronto: Pontifical Institute of Mediaeval Studies, 1985), pp. 89-90.
- ↑ David C. Lindberg, Theories of Vision from al-Kindi to Kepler, (Chicago: University of Chicago Pr., 1976), pp. 78–80, 98, 113–16
- ↑ Peter Marshall, "Nicole Oresme on the Nature, Reflection, and Speed of Light," Isis, 72 (1981): 357–374, pp. 360–2.
- ↑ Marshall Clagett, Nicole Oresme and the Medieval Geometry of Qualities and Motions (Madison: Univ. of Wisconsin Pr., 1968), pp. 164–211.
- ↑ Catholic Encyclopedia: "Nicole Oresme"
- ↑ Clagett, Marshall (editor & translator) (1968). Nicole Oresme and the Medieval Geometry of Qualities and Motions; a treatise on the uniformity and difformity of intensities known as Tractatus de configurationibus qualitatum et motuum. Madison, WI: University of Wisconsin Press. ISBN 0-299-04880-2.
- ↑ Pickover, Clifford A. (2009), The Math Book: From Pythagoras to the 57th Dimension, 250 Milestones in the History of Mathematics, Sterling Publishing Company, Inc., p. 104, ISBN 9781402757969,
Nicole Oresme ... was the first to prove the divergence of the harmonic series (c. 1350). His results were lost for several centuries, and the result was proved again by Italian mathematician Pietro Mengoli in 1647 and by Swiss mathematician Johann Bernoulli in 1687.
References
- Clagett, Marshall (1970). "Nicole Oresme" (PDF). In Gillispie, Charles. Dictionary of Scientific Biography 10. New York: Scribner & American Council of Learned Societies. pp. 223–240. ISBN 978-0-684-10114-9.
- Clagett, Marshall (1968). Nicole Oresme and the Medieval Geometry of Qualities and Motions: A Treatise on the Uniformity and Difformity of Intensities Known as Tractatus de configurationibus qualitatum at motuum. Madison: University of Wisconsin Press.
- Grant, Edward (1971). Nicole Oresme and the Kinematics of Circular Motion. Madison: University of Wisconsin Press. ISBN 0-299-05830-1.
- Hansen, Bert (1985). Nicole Oresme and the Marvels of Nature: A Study of his De causis mirabilium with Critical Edition, Translation, and Commentary. Pontifical Institute of Medieval Studies. ISBN 0-88844-068-5.
- Mäkeler, Hendrik (2003). "Nicolas Oresme und Gabriel Biel: Zur Geldtheorie im späten Mittelalter". Scripta Mercaturae: Zeitschrift für Wirtschafts- und Sozialgeschichte 37 (1): 56–94. (covers Oresme's monetary theory).
- Wood, Chauncey (1970). Chaucer and the Country of the Stars: Poetical Uses of Astrological Imagery. Princeton: Princeton University Press. ISBN 0-691-06172-6.
External links
| Wikiquote has quotations related to: Nicole Oresme |
| Wikimedia Commons has media related to Nicholas Oresme. |
- Works by or about Nicole Oresme at Internet Archive
- Kirschner, Stefan. "Stanford Encyclopedia of Philosophy"
|chapter=ignored (help). - O'Connor, John J.; Robertson, Edmund F.. "MacTutor History of Mathematics archive"
|chapter=ignored (help). - Oresme biography
- Article on Oresme's monetary theory
- The De Moneta of Nicholas Oresme and English Mint Documents (pdf)
- Tractatus de Origine, Natura, Jure et Mutationibus Monetarum (Latin)
| ||||||||||||||||||||||||||||||||||||||||||||
|