Newton's method in optimization

In calculus, Newton's method is an iterative method for finding the roots of a differentiable function  (i.e. solutions to the equation
(i.e. solutions to the equation 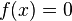 ). In optimization, Newton's method is applied to the derivative
). In optimization, Newton's method is applied to the derivative 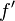 of a twice-differentiable function
of a twice-differentiable function  to find the roots of the derivative (solutions to
to find the roots of the derivative (solutions to 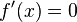 ), also known as the stationary points of
), also known as the stationary points of  .
.
Method
In the one-dimensional problem, Newton's Method attempts to construct a sequence 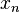 from an initial guess
from an initial guess 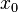 that converges towards
that converges towards 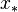 such that
such that 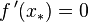 . This
. This 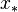 is a stationary point of
is a stationary point of  .
.
The second order Taylor expansion 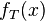 of
of  around
around 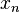 (where
(where 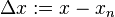 ) is:
) is:
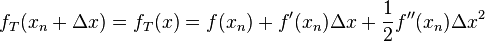 ,
,
and attains its extremum when its derivative with respect to 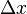 is equal to zero, i.e. when:
is equal to zero, i.e. when:
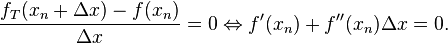
Thus, provided that 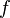 is a twice-differentiable function, the sequence
is a twice-differentiable function, the sequence 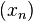 defined by:
defined by:
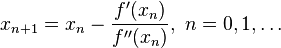
will converge towards a root of 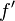 , i.e.
, i.e. 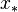 for which
for which 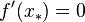 .
.
Geometric interpretation
The geometric interpretation of Newton's method is that at each iteration one approximates 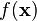 by a quadratic function around
by a quadratic function around 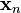 , and then takes a step towards the maximum/minimum of that quadratic function (in higher dimensions, this may also be a saddle point). Note that if
, and then takes a step towards the maximum/minimum of that quadratic function (in higher dimensions, this may also be a saddle point). Note that if 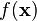 happens to be a quadratic function, then the exact extremum is found in one step.
happens to be a quadratic function, then the exact extremum is found in one step.
Higher dimensions
The above iterative scheme can be generalized to several dimensions by replacing the derivative with the gradient, 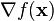 , and the reciprocal of the second derivative with the inverse of the Hessian matrix,
, and the reciprocal of the second derivative with the inverse of the Hessian matrix, 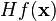 . One obtains the iterative scheme
. One obtains the iterative scheme
Usually Newton's method is modified to include a small step size 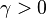 instead of
instead of 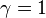
This is often done to ensure that the Wolfe conditions are satisfied at each step 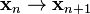 of the iteration.
of the iteration.
Where applicable, Newton's method converges much faster towards a local maximum or minimum than gradient descent. In fact, every local minimum has a neighborhood  such that, if we start with
such that, if we start with 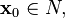 Newton's method with step size
Newton's method with step size 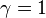 converges quadratically (if the Hessian is invertible and a Lipschitz continuous function of
converges quadratically (if the Hessian is invertible and a Lipschitz continuous function of 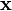 in that neighborhood).
in that neighborhood).
Finding the inverse of the Hessian in high dimensions can be an expensive operation. In such cases, instead of directly inverting the Hessian it's better to calculate the vector ![\mathbf{p}_{n} = [H f(\mathbf{x}_n)]^{-1} \nabla f(\mathbf{x}_n)](../I/m/46c319c012c56bd0693858b7d7f0c99b.png) as the solution to the system of linear equations
as the solution to the system of linear equations
which may be solved by various factorizations or approximately (but to great accuracy) using iterative methods. Many of these methods are only applicable to certain types of equations, for example the Cholesky factorization and conjugate gradient will only work if ![[H f(\mathbf{x}_n)]](../I/m/27a363a1016815d2010f8e3064f2d965.png) is a positive definite matrix. While this may seem like a limitation, it's often useful indicator of something gone wrong, for example if a minimization problem is being approached and
is a positive definite matrix. While this may seem like a limitation, it's often useful indicator of something gone wrong, for example if a minimization problem is being approached and ![[H f(\mathbf{x}_n)]](../I/m/27a363a1016815d2010f8e3064f2d965.png) is not positive definite, then the iterations are converging to a saddle point and not a minimum.
is not positive definite, then the iterations are converging to a saddle point and not a minimum.
On the other hand, if a constrained optimization is done (for example, with Lagrange multipliers), the problem may become one of saddle point finding, in which case the Hessian will be symmetric indefinite and the solution of 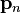 will need to be done with a method that will work for such, such as the LDLT variant of Cholesky factorization or the conjugate residual method.
will need to be done with a method that will work for such, such as the LDLT variant of Cholesky factorization or the conjugate residual method.
There also exist various quasi-Newton methods, where an approximation for the Hessian (or its inverse directly) is built up from changes in the gradient.
If the Hessian is close to a non-invertible matrix, the inverted Hessian can be numerically unstable and the solution may diverge. In this case, certain workarounds have been tried in the past, which have varied success with certain problems. One can, for example, modify the Hessian by adding a correction matrix 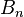 so as to make
so as to make 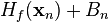 positive definite. One approach is to diagonalize
positive definite. One approach is to diagonalize 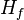 and choose
and choose 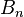 so that
so that 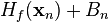 has the same eigenvectors as
has the same eigenvectors as 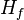 , but with each negative eigenvalue replaced by
, but with each negative eigenvalue replaced by 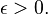
An approach exploited in the Levenberg–Marquardt algorithm (which uses an approximate Hessian) is to add a scaled identity matrix to the Hessian, 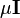 , with the scale adjusted at every iteration as needed. For large
, with the scale adjusted at every iteration as needed. For large  and small Hessian, the iterations will behave like gradient descent with step size
and small Hessian, the iterations will behave like gradient descent with step size  . This results in slower but more reliable convergence where the Hessian doesn't provide useful information.
. This results in slower but more reliable convergence where the Hessian doesn't provide useful information.
See also
- Quasi-Newton method
- Gradient descent
- Gauss–Newton algorithm
- Levenberg–Marquardt algorithm
- Trust region
- Optimization
- Nelder–Mead method
Notes
References
- Avriel, Mordecai (2003). Nonlinear Programming: Analysis and Methods. Dover Publishing. ISBN 0-486-43227-0.
- Bonnans, J. Frédéric; Gilbert, J. Charles; Lemaréchal, Claude; Sagastizábal, Claudia A. (2006). Numerical optimization: Theoretical and practical aspects. Universitext (Second revised ed. of translation of 1997 French ed.). Berlin: Springer-Verlag. pp. xiv+490. doi:10.1007/978-3-540-35447-5. ISBN 3-540-35445-X. MR 2265882.
- Fletcher, Roger (1987). Practical methods of optimization (2nd ed.). New York: John Wiley & Sons. ISBN 978-0-471-91547-8..
- Nocedal, Jorge & Wright, Stephen J. (1999). Numerical Optimization. Springer-Verlag. ISBN 0-387-98793-2.
- "Newton-Raphson visualization (1D)"..
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
![\mathbf{x}_{n+1} = \mathbf{x}_n - [H f(\mathbf{x}_n)]^{-1} \nabla f(\mathbf{x}_n), \ n \ge 0.](../I/m/a3403b4fe483dcb2667bbf7bbcb221d6.png)
![\mathbf{x}_{n+1} = \mathbf{x}_n - \gamma[H f(\mathbf{x}_n)]^{-1} \nabla f(\mathbf{x}_n).](../I/m/f16caa97e948bb3d32f521ebadbb7279.png)
![[H f(\mathbf{x}_n)] \mathbf{p}_{n} = \nabla f(\mathbf{x}_n)](../I/m/c7447e3a9b1585057f6d29e671b8a0e5.png)
