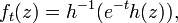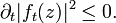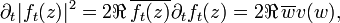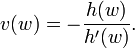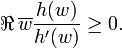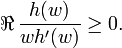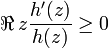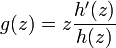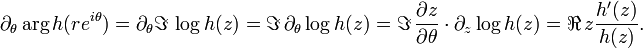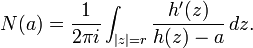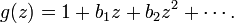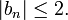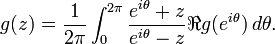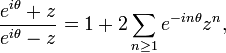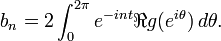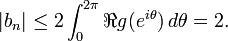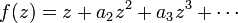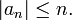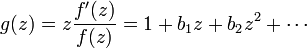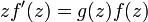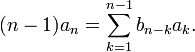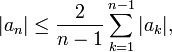Nevanlinna's criterion
In mathematics, Nevanlinna's criterion in complex analysis, proved in 1920 by the Finnish mathematician Rolf Nevanlinna, characterizes holomorphic univalent functions on the unit disk which are starlike. Nevanlinna used this criterion to prove the Bieberbach conjecture for starlike univalent functions
Statement of criterion
A univalent function h on the unit disk satisfying h(0) = 0 and h'(0) = 1 is starlike, i.e. has image invariant under multilpication by real numbers in [0,1], if and only if 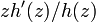 has positive real part for |z| < 1 and takes the value 1 at 0.
has positive real part for |z| < 1 and takes the value 1 at 0.
Note that, by applying the result to a•h(rz), the criterion applies on any disc |z| < r with only the requirement that f(0) = 0 and f'(0) ≠ 0.
Proof of criterion
Let h(z) be a starlike univalent function on |z| < 1 with h(0) = 0 and h'(0) = 1.
For t < 0, define[1]
a semigroup of holomorphic mappinga of D into itself fixing 0.
Moreover h is the Koenigs function for the semigroup ft.
By the Schwarz lemma, |ft(z)| decreases as t increases.
Hence
But, setting w = ft(z),
where
Hence
and so, dividing by |w|2,
Taking reciprocals and letting t go to 0 gives
for all |z| < 1. Since the left hand side is a harmonic function, the maximum principle implies the inequality is strict.
Conversely if
has positive real part and g(0) = 1, then h can vanish only at 0, where it must have a simple zero.
Now
Thus as z traces the circle 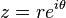 , the argument of the image
, the argument of the image 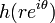 increases strictly. By the argument principle, since
increases strictly. By the argument principle, since 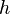 has a simple zero at 0,
it circles the origin just once. The interior of the region bounded by the curve it traces is therefore starlike. If a is a point in the interior then the number of solutions N(a) of h(z) = a with |z| < r is given by
has a simple zero at 0,
it circles the origin just once. The interior of the region bounded by the curve it traces is therefore starlike. If a is a point in the interior then the number of solutions N(a) of h(z) = a with |z| < r is given by
Since this is an integer, depends continuously on a and N(0) = 1, it is identically 1. So h is univalent and starlike in each disk |z| < r and hence everywhere.
Application to Bieberbach conjecture
Carathéodory's lemma
Constantin Carathéodory proved in 1907 that if
is a holomorphic function on the unit disk D with positive real part, then[2][3]
In fact it suffices to show the result with g replaced by gr(z) = g(rz) for any r < 1 and then pass to the limit r = 1. In that case g extends to a continuous function on the closed disc with positive real part and by Schwarz formula
Using the identity
it follows that
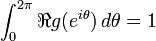 ,
,
so defines a probability measure, and
Hence
Proof for starlike functions
Let
be a univalent starlike function in |z| < 1. Nevanlinna (1921) proved that
In fact by Nevanlinna's criterion
has positive real part for |z|<1. So by Carathéodory's lemma
On the other hand
gives the recurrence relation
where a1 = 1. Thus
so it follows by induction that
Notes
- ↑ Hayman 1994, p. 14
- ↑ Duren 1982, p. 41
- ↑ Pommerenke 1975, p. 40
References
- Carathéodory, C. (1907), "Über den Variabilitatsbereich der Koeffizienten von Potenzreihen, die gegebene Werte nicht annehmen", Math. Ann. 64: 95–115, doi:10.1007/bf01449883
- Duren, P. L. (1983), Univalent functions, Grundlehren der Mathematischen Wissenschaften 259, Springer-Verlag, pp. 41–42, ISBN 0-387-90795-5
- Hayman, W. K. (1994), Multivalent functions, Cambridge Tracts in Mathematics 110 (2nd ed.), Cambridge University Press, ISBN 0-521-46026-3
- Nevanlinna, R. (1921), "Über die konforme Abbildung von Sterngebieten", Ofvers. Finska Vet. Soc. Forh. 53: 1–21
- Pommerenke, C. (1975), Univalent functions, with a chapter on quadratic differentials by Gerd Jensen, Studia Mathematica/Mathematische Lehrbücher 15, Vandenhoeck & Ruprecht