Neutral sixth
| Inverse | neutral third |
|---|---|
| Name | |
| Other names | - |
| Abbreviation | n6 |
| Size | |
| Semitones | ~8½ |
| Interval class | ~3½ |
| Just interval | 18:11[1] or 13:8[2] |
| Cents | |
| Equal temperament | 800 or 900 |
| Just intonation | 853 or 841 |
Play .A neutral sixth is a musical interval wider than a minor sixth play but narrower than a major sixth play . Three distinct intervals may be termed neutral sixths:
- The undecimal neutral sixth has a ratio of 18:11 between the frequencies of the two tones, or about 852.59 cents. play
- A tridecimal neutral sixth has a ratio of 13:8 between the frequencies of the two tones, or about 840.53 cents.[3] This is the smallest neutral sixth, and occurs infrequently in music, as little music utilizes the 13th harmonic. play
- An equal-tempered neutral sixth is 850 cents, a hair narrower than the 18:11 ratio. It is an equal-tempered quarter tone exactly half way between the equal-tempered minor and major sixths, and half of an equal-tempered perfect eleventh (octave plus fourth). play
These intervals are all within about 12 cents of each other and are difficult for most people to distinguish. Neutral sixths are roughly a quarter tone sharp from 12 equal temperament minor sixths and a quarter tone flat from 12-ET major sixths. In just intonation, as well as in tunings such as 31-ET, 41-ET, or 72-ET, which more closely approximate just intonation, the intervals are closer together.
A neutral sixth can be formed by subtracting a neutral second from a minor seventh. Based on its positioning in the harmonic series, the undecimal neutral sixth implies a root one minor seventh above the higher of the two notes.
Thirteenth harmonic
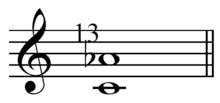
Play 13:8 (840.53 cents), the ratio of the thirteenth harmonic is notated in Ben Johnston's system as A13♭.
This note is often corrected to a just or pythagorean ratio on the natural horn, but the pure thirteenth harmonic was used in pieces including Britten's Serenade for tenor, horn and strings.[4]
See also
References
- ↑ Haluska, Jan (2003). The Mathematical Theory of Tone Systems, p.xxiv. ISBN 0-8247-4714-3. Undecimal neutral sixth.
- ↑ Haluska (2003), p.xxiii. Tridecimal neutral sixth.
- ↑ Jan Haluska, The Mathematical Theory of Tone Systems, CRC (2004).
- ↑ Fauvel, John; Flood, Raymond; and Wilson, Robin J. (2006). Music And Mathematics, p.21-22. ISBN 9780199298938.
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||