Nernst–Planck equation

The time dependent form of the Nernst–Planck equation is a conservation of mass equation used to describe the motion of a charged chemical species in a fluid medium. It describes the flux of ions under the influence of both an ionic concentration gradient 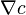$\nabla c$ and an electric field 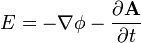$E=-\nabla \phi - \frac{\partial \mathbf A}{\partial t}$ . It extends Fick's law of diffusion for the case where the diffusing particles are also moved with respect to the fluid by electrostatic forces:^[1]^[2]

$\frac{\partial c}{\partial t} = \nabla \cdot \left[ D \nabla c - u c + \frac{Dze}{k_B T}c(\nabla \phi+\frac{\partial \mathbf A}{\partial t}) \right]$

Where

t is time,
D is the diffusivity of the chemical species,
c is the concentration of the species, and u is the velocity of the fluid,
z is the valence of ionic species,
e is the elementary charge,
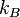$k_B$ is the Boltzmann constant
T is the temperature.
u is relative velocity of the observer to the ionic system

If the diffusing particles are themselves charged they influence the electric field on moving. Hence the Nernst–Planck equation is applied in describing the ion-exchange kinetics in soils.^[3]

In the context of Neuroscience, this equation is best known in its steady-state form, where there is a balance of diffusion and drift. Setting time derivatives to zero, and noting that the term 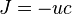$J = -uc$ represents a current flux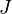 $J$

$\nabla \cdot \left[ D \nabla c + J + \frac{Dze}{k_B T}c(\nabla \phi) \right]= 0$

Integrating the divergence over an arbitrary surface, one obtains the steady state Nernst-Planck equation

$J = -\left[ D \nabla c + \frac{Dze}{k_B T}c(\nabla \phi) \right]$

Finally, in units of 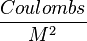$\frac{Coulombs}{M^2}$ and the gas constant R, one obtains the more familiar form (e.g. ^[4]

$J = -zFD\left[ \nabla c + \frac{Fzc}{RT}(\nabla \phi) \right]$

Notes

↑ Kirby BJ. (2010). Micro- and Nanoscale Fluid Mechanics: Transport in Microfluidic Devices: Chapter 11: Species and Charge Transport.
↑ Probstein R (1994). Physicochemical Hydrodynamics.
↑ Sparks, D.L. (1988). "Kinetics of Soil Chemical Processes.". Academic Press, New York. pp. 101ff.
↑ B. Hille (1992) Ionic Channels of Excitable Media, 2nd Edition, Sinauer, Sunderland Mass. p.267

Nernst–Planck equation

See also

Notes