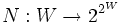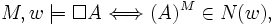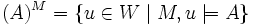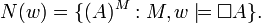Neighborhood semantics

Neighborhood semantics, also known as Scott-Montague semantics, is a formal semantics for modal logics. It is a generalization, developed independently by Dana Scott and Richard Montague, of the more widely known relational semantics for modal logic. Whereas a relational frame 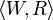\langle W,R\rangle consists of a set W of worlds (or states) and an accessibility relation R intended to indicate which worlds are alternatives to (or, accessible from) others, a neighborhood frame 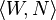\langle W,N\rangle still has a set W of worlds, but has instead of an accessibility relation a neighborhood function

N : W \to 2^{2^W}

that assigns to each element of W a set of subsets of W. Intuitively, each family of subsets assigned to a world are the propositions necessary at that world, where 'proposition' is defined as a subset of W (i.e. the set of worlds at which the proposition is true). Specifically, if M is a model on the frame, then

M,w\models\square A \Longleftrightarrow (A)^M \in N(w),

where

(A)^M = \{u\in W \mid M,u\models A \}

is the truth set of A.

Neighborhood semantics is used for the classical modal logics that are strictly weaker than the normal modal logic K.

Correspondence between relational and neighborhood models

To every relational model M = (W,R,V) there corresponds an equivalent (in the sense of having point-wise equivalent modal theories) neighborhood model M' = (W,N,V) defined by

N(w) = \{(A)^M: M,w\models\Box A\}.

The fact that the converse fails gives a precise sense to the remark that neighborhood models are a generalization of relational ones. Another (perhaps more natural) generalization of relational structures are general relational structures.

References