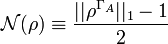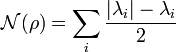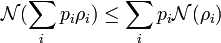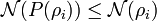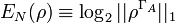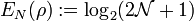Negativity (quantum mechanics)
In quantum mechanics, negativity is a measure of quantum entanglement which is easy to compute. It is a measure deriving from the PPT criterion for separability.[1] It has shown to be an entanglement monotone [2][3] and hence a proper measure of entanglement.
Definition
The negativity of a subsystem 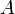 can be defined in terms of a density matrix
can be defined in terms of a density matrix 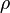 as:
as:
where:
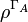 is the partial transpose of
is the partial transpose of 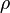 with respect to subsystem
with respect to subsystem 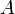
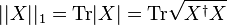 is the trace norm or the sum of the singular values of the operator
is the trace norm or the sum of the singular values of the operator 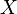 .
.
An alternative and equivalent definition is the absolute sum of the negative eigenvalues of 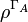 :
:
where 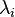 are all of the eigenvalues.
are all of the eigenvalues.
Properties
- Is a convex function of
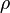 :
:
- Is an entanglement monotone:
where 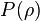 is an arbitrary LOCC operation over
is an arbitrary LOCC operation over 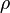
Logarithmic negativity
The logarithmic negativity is an entanglement measure which is easily computable and an upper bound to the distillable entanglement.[4] It is defined as
where 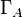 is the partial transpose operation and
is the partial transpose operation and 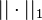 denotes the trace norm.
denotes the trace norm.
It relates to the negativity as follows:[1]
Properties
The logarithmic negativity
- can be zero even if the state is entangled (if the state is PPT entangled).
- does not reduce to the entropy of entanglement on pure states like most other entanglement measures.
- is additive on tensor products:
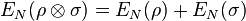
- is not asymptotically continuous. That means that for a sequence of bipartite Hilbert spaces
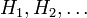 (typically with increasing dimension) we can have a sequence of quantum states
(typically with increasing dimension) we can have a sequence of quantum states 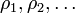 which converges to
which converges to 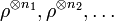 (typically with increasing
(typically with increasing 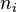 ) in the trace distance, but the sequence
) in the trace distance, but the sequence 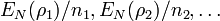 does not converge to
does not converge to 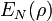 .
. - is an upper bound to the distillable entanglement
References
- This page uses material from Quantwiki licensed under GNU Free Documentation License 1.2
- ↑ 1.0 1.1 K. Zyczkowski, P. Horodecki, A. Sanpera, M. Lewenstein (1998). "Volume of the set of separable states". Phys. Rev. 883 A 58. arXiv:quant-ph/9804024. Bibcode:1998PhRvA..58..883Z. doi:10.1103/PhysRevA.58.883. Retrieved 24 January 2015.
- ↑ J. Eisert (2001). Entanglement in quantum information theory (Thesis). University of Potsdam.
- ↑ G. Vidal, R. F. Werner (2002). "A computable measure of entanglement". Phys. Rev. 032314 A 65. arXiv:quant-ph/0102117. Bibcode:2002PhRvA..65c2314V. doi:10.1103/PhysRevA.65.032314. Retrieved 24 March 2012.
- ↑ M. B. Plenio (2005). "The logarithmic negativity: A full entanglement monotone that is not convex". Phys. Rev. Lett. 090503 95. arXiv:quant-ph/0505071. Bibcode:2005PhRvL..95i0503P. doi:10.1103/PhysRevLett.95.090503. Retrieved 24 March 2012.