Negative multinomial distribution
| Notation |
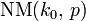 |
|---|---|
| Parameters |
k0 ∈ N0 — the number of failures before the experiment is stopped, p0 = 1 − (p1+…+pm) — the probability of a “failure”. |
| Support |
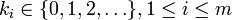 |
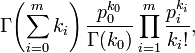 where Γ(x) is the Gamma function. | |
| Mean |
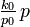 |
| Variance |
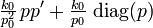 |
| CF |
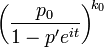 |
In probability theory and statistics, the negative multinomial distribution is a generalization of the negative binomial distribution (NB(r, p)) to more than two outcomes.[1]
Suppose we have an experiment that generates m+1≥2 possible outcomes, {X0,…,Xm}, each occurring with non-negative probabilities {p0,…,pm} respectively. If sampling proceeded until n observations were made, then {X0,…,Xm} would have been multinomially distributed. However, if the experiment is stopped once X0 reaches the predetermined value k0, then the distribution of the m-tuple {X1,…,Xm} is negative multinomial. These variables are not multinomially distributed because their sum X1+…+Xm is not fixed, being a draw from a negative binomial distribution.
Negative multinomial distribution example
The table below shows the an example of 400 Melanoma (skin cancer) Patients where the Type and Site of the cancer are recorded for each subject.
| Type | Site | Totals | ||
| Head and Neck | Trunk | Extremities | ||
| Hutchinson's melanomic freckle | 22 | 2 | 10 | 34 |
| Superficial | 16 | 54 | 115 | 185 |
| Nodular | 19 | 33 | 73 | 125 |
| Indeterminant | 11 | 17 | 28 | 56 |
| Column Totals | 68 | 106 | 226 | 400 |
The sites (locations) of the cancer may be independent, but there may be positive dependencies of the type of cancer for a given location (site). For example, localized exposure to radiation implies that elevated level of one type of cancer (at a given location) may indicate higher level of another cancer type at the same location. The Negative Multinomial distribution may be used to model the sites cancer rates and help measure some of the cancer type dependencies within each location.
If  denote the cancer rates for each site (
denote the cancer rates for each site ( ) and each type of cancer (
) and each type of cancer (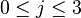 ), for a fixed site (
), for a fixed site (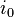 ) the cancer rates are independent Negative Multinomial distributed random variables. That is, for each column index (site) the column-vector X has the following distribution:
) the cancer rates are independent Negative Multinomial distributed random variables. That is, for each column index (site) the column-vector X has the following distribution:
-
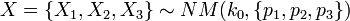 .
.
Different columns in the table (sites) are considered to be different instances of the random multinomially distributed vector, X. Then we have the following estimates of expected counts (frequencies of cancer):
-
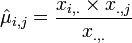
-
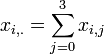
-
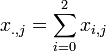
-
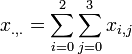
- Example:
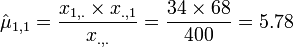
For the first site (Head and Neck, j=0), suppose that 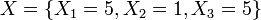 and
and 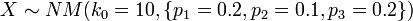 . Then:
. Then:
-
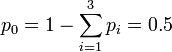
-
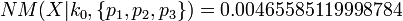
-
![cov[X_1,X_3] = \frac{10 \times 0.2 \times 0.2}{0.5^2}=1.6](../I/m/3856250206cbbc14e0a5711c107d924f.png)
-
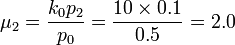
-
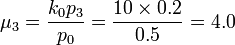
-
![corr[X_2,X_3] = \left (\frac{\mu_2 \times \mu_3}{(k_0+\mu_2)(k_0+\mu_3)} \right )^{\frac{1}{2}}](../I/m/8a0eed030df471cf1d24d18932b436c4.png) and therefore,
and therefore, ![corr[X_2,X_3] = \left (\frac{2 \times 4}{(10+2)(10+4)} \right )^{\frac{1}{2}} = 0.21821789023599242.](../I/m/936f6ecdb9cfbd2dc64f7c0d874ed47d.png)
Notice that the pair-wise NM correlations are always positive, whereas the correlations between multinomial counts are always negative. As the parameter  increases, the paired correlations tend to zero! Thus, for large
increases, the paired correlations tend to zero! Thus, for large  , the Negative Multinomial counts
, the Negative Multinomial counts  behave as independent Poisson random variables with respect to their means
behave as independent Poisson random variables with respect to their means 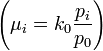 .
.
The marginal distribution of each of the  variables is negative binomial, as the
variables is negative binomial, as the  count (considered as success) is measured against all the other outcomes (failure). But jointly, the distribution of
count (considered as success) is measured against all the other outcomes (failure). But jointly, the distribution of 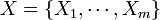 is negative multinomial, i.e.,
is negative multinomial, i.e., 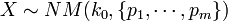 .
.
Parameter estimation
- Estimation of the mean (expected) frequency counts (
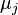 ) of each outcome (
) of each outcome (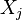 ) using maximum likelihood is possible. If we have a single observation vector
) using maximum likelihood is possible. If we have a single observation vector 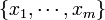 , then
, then 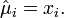 If we have several observation vectors, like in this case we have the cancer type frequencies for 3 different sites, then the MLE estimates of the mean counts are
If we have several observation vectors, like in this case we have the cancer type frequencies for 3 different sites, then the MLE estimates of the mean counts are 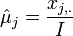 , where
, where 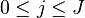 is the cancer-type index and the summation is over the number of observed (sampled) vectors (I). For the cancer data above, we have the following MLE estimates for the expectations for the frequency counts:
is the cancer-type index and the summation is over the number of observed (sampled) vectors (I). For the cancer data above, we have the following MLE estimates for the expectations for the frequency counts:
- Hutchinson's melanomic freckle type of cancer (
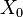 ) is
) is 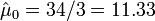 .
. - Superficial type of cancer (
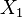 ) is
) is 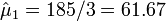 .
. - Nodular type of cancer (
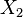 ) is
) is 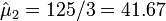 .
. - Indeterminant type of cancer (
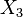 ) is
) is 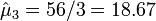 .
.
- Hutchinson's melanomic freckle type of cancer (
- There is no MLE estimate for the NM
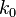 parameter.[1][2] However, there are approximate protocols for estimating the
parameter.[1][2] However, there are approximate protocols for estimating the 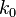 parameter using the chi-squared goodness of fit statistic. In the usual chi-squared statistic:
parameter using the chi-squared goodness of fit statistic. In the usual chi-squared statistic:
-
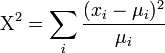 , we can replace the expected-means (
, we can replace the expected-means (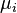 ) by their estimates,
) by their estimates, 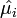 , and replace denominators by the corresponding negative multinomial variances. Then we get the following test statistic for negative multinomial distributed data:
, and replace denominators by the corresponding negative multinomial variances. Then we get the following test statistic for negative multinomial distributed data: -
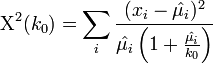 .
.
- Next, we can estimate the
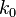 parameter by varying the values of
parameter by varying the values of 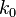 in the expression
in the expression 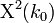 and matching the values of this statistic with the corresponding asymptotic chi-squared distribution. The following protocol summarizes these steps using the cancer data above.
and matching the values of this statistic with the corresponding asymptotic chi-squared distribution. The following protocol summarizes these steps using the cancer data above.
- DF: The degree of freedom for the Chi-squared distribution in this case is:
- df = (# rows – 1)(# columns – 1) = (3-1)*(4-1) = 6
- DF: The degree of freedom for the Chi-squared distribution in this case is:
- Median: The median of a chi-squared random variable with 6 df is 5.261948.
- Mean Counts Estimates: The mean counts estimates (
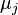 ) for the 4 different cancer types are:
) for the 4 different cancer types are:
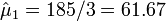 ;
; 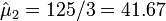 ; and
; and 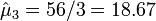 .
.
- Mean Counts Estimates: The mean counts estimates (
- Thus, we can solve the equation above
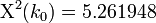 for the single variable of interest -- the unknown parameter
for the single variable of interest -- the unknown parameter 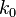 . In the cancer example, suppose
. In the cancer example, suppose 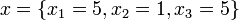 . Then, the solution is an asymptotic chi-squared distribution driven estimate of the parameter
. Then, the solution is an asymptotic chi-squared distribution driven estimate of the parameter 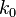 .
. -
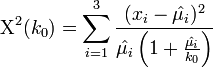 .
. -
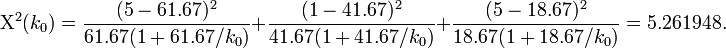 Solving this equation for
Solving this equation for 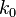 provides the desired estimate for the last parameter.
provides the desired estimate for the last parameter.
- Mathematica provides 3 distinct (
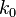 ) solutions to this equation: {50.5466, -21.5204, 2.40461}. Since
) solutions to this equation: {50.5466, -21.5204, 2.40461}. Since 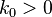 there are 2 candidate solutions.
there are 2 candidate solutions.
- Mathematica provides 3 distinct (
- Estimates of probabilities: Assume
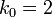 and
and 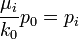 , then:
, then:
-
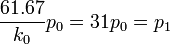
-
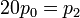
-
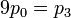
- Hence,
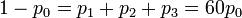 , and
, and 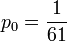 ,
, 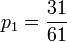 ,
, 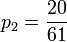 and
and 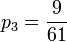 .
. - Therefore, the best model distribution for the observed sample
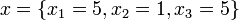 is
is 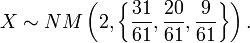
Related distributions
- Negative binomial distribution
- Multinomial distribution
- Inverted Dirichlet distribution, a conjugate prior for the negative multinomial
References
- ↑ 1.0 1.1 Le Gall, F. The modes of a negative multinomial distribution, Statistics & Probability Letters, Volume 76, Issue 6, 15 March 2006, Pages 619-624, ISSN 0167-7152, 10.1016/j.spl.2005.09.009.
- ↑ Zelterman, Daniel (2002). Advanced log-linear models using SAS. SAS Publishing. p. 196. ISBN 978-1-59047-080-0.
Waller LA and Zelterman D. (1997). Log-linear modeling with the negative multi- nomial distribution. Biometrics 53: 971-82.
Further reading
Johnson, Norman L.; Kotz, Samuel; Balakrishnan, N. (1997). "Chapter 36: Negative Multinomial and Other Multinomial-Related Distributions". Discrete Multivariate Distributions. Wiley. ISBN 0-471-12844-9.