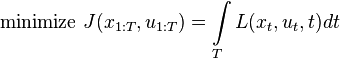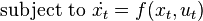Navigation function

Navigation function usually refers to a function of position, velocity, acceleration and time which is used to plan robot trajectories through the environment. Generally, the goal of a navigation function is to create feasible, safe paths that avoid obstacles while allowing a robot to move from its starting configuration to its goal configuration.

Potential functions as navigation functions

A potential function. Imagine dropping a marble on the surface. It will avoid the three obstacles and eventually reach the goal position in the center.

Potential functions assume that the environment or work space is known. Obstacles are assigned a high potential value, and the goal position is assigned a low potential. To reach the goal position, a robot only needs to follow the negative gradient of the surface.

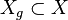We can formalize this concept mathematically as following: Let X be the state space of all possible configurations of a robot. Let X_g \subset X denote the goal region of the state space.

Then a potential function 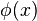\phi(x) is called a (feasible) navigation function if [1]

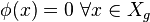
  1. \phi(x)=0\ \forall x \in X_g
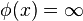  2. \phi(x) = \infty if and only if no point in 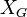{X_{G}} is reachable from x.
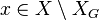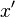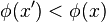  3. For every reachable state, x \in X \setminus {X_{G}}, the local operator produces a state x' for which \phi(x') < \phi(x).

Navigation Function in Optimal Control

While for certain applications, it suffices to have a feasible navigation function, in many cases it is desirable to have an optimal navigation function with respect to a given cost functional 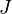J. Formalized as an optimal control problem, we can write

\text{minimize } J(x_{1:T},u_{1:T})=\int\limits_T L(x_t,u_t,t) dt
\text{subject to } \dot{x_t} = f(x_t,u_t)

whereby x is the state, u is the control to apply, L is a cost at a certain state x if we apply a control u, and f models the transition dynamics of the system.

Applying Bellman's principle of optimality the optimal cost-to-go function is defined as

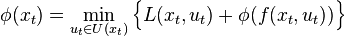
\displaystyle \phi(x_t) = \min_{u_t \in U(x_t)} \Big\{ L(x_t,u_t) + \phi(f(x_t,u_t)) \Big\}

Together with the above defined axioms we can define the optimal navigation function as

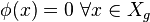
  1. \phi(x)=0\ \forall x \in X_g
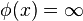  2. \phi(x) = \infty if and only if no point in 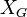{X_{G}} is reachable from x.
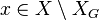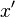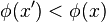  3. For every reachable state, x \in X \setminus {X_{G}}, the local operator produces a state x' for which \phi(x') < \phi(x).
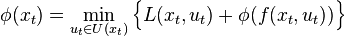
  4. \displaystyle \phi(x_t) = \min_{u_t \in U(x_t)} \Big\{ L(x_t,u_t) + \phi(f(x_t,u_t)) \Big\}

Stochastic Navigation Function

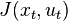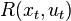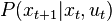If we assume the transition dynamics of the system or the cost function as subjected to noise, we obtain a stochastic optimal control problem with a cost J(x_t,u_t) and dynamics f. In the field of reinforcement learning the cost is replaced by a reward function R(x_t,u_t) and the dynamics by the transition probabilities P(x_{t+1}|x_t,u_t).

See also

References

External links

References

  1. ↑ Lavalle, Steven, Planning Algorithms Chapter 8