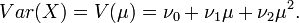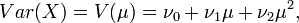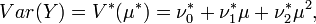Natural exponential family
In probability and statistics, a natural exponential family (NEF) is a class of probability distributions that is a special case of an exponential family (EF). Every distribution possessing a moment-generating function is a member of a natural exponential family, and the use of such distributions simplifies the theory and computation of generalized linear models.
Definition
Probability distribution function (PDF) of the univariate case (scalar domain, scalar parameter)
The natural exponential family (NEF) is a subset of the exponential family. NEF is an exponential family in which the natural parameter η and the natural statistic T(x) are both the identity. A distribution in the exponential family with parameter θ can be written with probability density function (PDF)
where  and
and 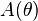 are known functions.
A distribution in the natural exponential family with parameter θ can thus be written with PDF
are known functions.
A distribution in the natural exponential family with parameter θ can thus be written with PDF
[Note that slightly different notation is used by the originator of the NEF, Carl Morris.[1] Morris uses ω instead of η and ψ instead of A.]
Probability distribution function (PDF) of the general case (multivariate domain and/or parameter)
Suppose that 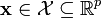 , then a natural exponential family of order p has density or mass function of the form:
, then a natural exponential family of order p has density or mass function of the form:
where in this case the parameter 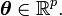
Moment and cumulant generating function
A member of a natural exponential family has moment generating function (MGF) of the form
The cumulant generating function is by definition the logarithm of the MGF, so it is
Examples
The five most important univariate cases are:
- normal distribution with known variance
- Poisson distribution
- gamma distribution with known shape parameter α (or k depending on notation set used)
- binomial distribution with known number of trials, n
- negative binomial distribution with known

These five examples – Poisson, binomial, negative binomial, normal, and gamma – are a special subset of NEF, called NEF with quadratic variance function (NEF-QVF) because the variance can be written as a quadratic function of the mean. NEF-QVF are discussed below.
Distributions such as the exponential, chi-squared, Rayleigh, Weibull, Bernoulli, and geometric distributions are special cases of the above five distributions. Many common distributions are either NEF or can be related to the NEF. For example: the chi-squared distribution is a special case of the gamma distribution. The Bernoulli distribution is a binomial distribution with n = 1 trial. The exponential distribution is a gamma distribution with shape parameter α = 1 (or k = 1 ). The Rayleigh and Weibull distributions can each be written in terms of an exponential distribution.
Some exponential family distributions are not NEF. The lognormal and Beta distribution are in the exponential family, but not the natural exponential family.
The parameterization of most of the above distributions has been written differently from the parameterization commonly used in textbooks and the above linked pages. For example, the above parameterization differs from the parameterization in the linked article in the Poisson case. The two parameterizations are related by 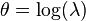 , where λ is the mean parameter, and so that the density may be written as
, where λ is the mean parameter, and so that the density may be written as
for 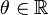 , so
, so
 , and
, and 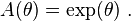
This alternative parameterization can greatly simplify calculations in mathematical statistics. For example, in Bayesian inference, a posterior probability distribution is calculated as the product of two distributions. Normally this calculation requires writing out the probability distribution functions (PDF) and integrating; with the above parameterization, however, that calculation can be avoided. Instead, relationships between distributions can be abstracted due to the properties of the NEF described below.
An example of the multivariate case is the multinomial distribution with known number of trials.
Properties
The properties of the natural exponential family can be used to simplify calculations involving these distributions.
Univariant case
1. The cumulants of an NEF can be calculated as derivatives of the NEF's cumulant generating function. The nth cumulant is the nth derivative with respect to θ of the cumulant generating function.
The cumulant generating function is
The first cumulant is
The mean is the first moment and always equal to the first cumulant, so
The variance is always the second moment, and it is always related to the first and second cumulants by
so that
The nth cumulant is
2. Natural exponential families (NEF) are closed under convolution.
Given independent identically distributed (iid) 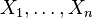 with distribution from an NEF, then
with distribution from an NEF, then 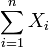 is an NEF, although not necessarily the original NEF. This follows from the properties of the cumulant generating function.
is an NEF, although not necessarily the original NEF. This follows from the properties of the cumulant generating function.
3. The variance function for random variables with an NEF distribution can be written in terms of the mean.
4. The first two moments of a NEF distribution uniquely specify the distribution within that family of distributions.
Multivariate case
In the multivariate case, the mean vector and covariance matrix are
![\mathrm{E}[X] = \nabla A(\boldsymbol\theta)\,](../I/m/a9361fffaa1d9d931f0d8b2d617769e5.png) and
and ![\mathrm{Cov}[X] = \nabla \nabla^{\rm T} A(\boldsymbol\theta)\, ,](../I/m/62e78444792b7bfac05b861ca1732c4f.png)
where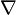 is the gradient and
is the gradient and 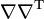 is the Hessian matrix.
is the Hessian matrix.
Natural exponential families with quadratic variance functions (NEF-QVF)
A special case of the natural exponential families are those with quadratic variance functions. Six NEFs have quadratic variance functions (QVF) in which the variance of the distribution can be written as a quadratic function of the mean. These are called NEF-QVF. The properties of these distributions were first described by Carl Morris.[2]
The six NEF-QVFs
The six NEF-QVF are written here in increasing complexity of the relationship between variance and mean.
1. The normal distribution with fixed variance 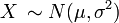 is NEF-QVF because the variance is constant. The variance can be written
is NEF-QVF because the variance is constant. The variance can be written 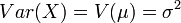 , so variance is a degree 0 function of the mean.
, so variance is a degree 0 function of the mean.
2. The Poisson distribution 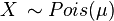 is NEF-QVF because all Poisson distributions have variance equal to the mean
is NEF-QVF because all Poisson distributions have variance equal to the mean 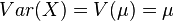 , so variance is a linear function of the mean.
, so variance is a linear function of the mean.
3. The Gamma distribution 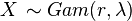 is NEF-QVF because the mean of the Gamma distribution is
is NEF-QVF because the mean of the Gamma distribution is 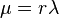 and the variance of the Gamma distribution is
and the variance of the Gamma distribution is 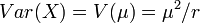 , so the variance is a quadratic function of the mean.
, so the variance is a quadratic function of the mean.
4. The binomial distribution 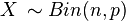 is NEF-QVF because the mean is
is NEF-QVF because the mean is  and the variance is
and the variance is 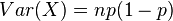 which can be written in terms of the mean as
which can be written in terms of the mean as

5. The negative binomial distribution 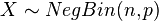 is NEF-QVF because the mean is
is NEF-QVF because the mean is 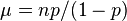 and the variance is
and the variance is

6. The (not very famous) distribution generated by the generalized hyperbolic secant distribution (NEF-GHS) has
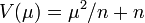 and
and 
Properties of NEF-QVF
The properties of NEF-QVF can simplify calculations that use these distributions.
1. Natural exponential families with quadratic variance functions (NEF-QVF) are closed under convolutions of a linear transformation. That is, a convolution of a linear transformation of an NEF-QVF is also an NEF-QVF, although not necessarily the original one.
Given independent identically distributed (iid) 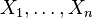 with distribution from a NEF-QVF. A convolution of a linear transformation of an NEF-QVF is also an NEF-QVF.
with distribution from a NEF-QVF. A convolution of a linear transformation of an NEF-QVF is also an NEF-QVF.
Let 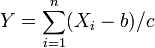 be the convolution of a linear transformation of X.
The mean of Y is
be the convolution of a linear transformation of X.
The mean of Y is 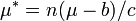 . The variance of Y can be written in terms of the variance function of the original NEF-QVF. If the original NEF-QVF had variance function
. The variance of Y can be written in terms of the variance function of the original NEF-QVF. If the original NEF-QVF had variance function
then the new NEF-QVF has variance function
where
2. Let 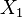 and
and 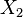 be independent NEF with the same parameter θ and let
be independent NEF with the same parameter θ and let  . Then the conditional distribution of
. Then the conditional distribution of 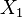 given Y
given Y  has quadratic variance in Y if and only if
has quadratic variance in Y if and only if 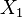 and
and 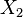 are NEF-QVF. Examples of conditional distributions
are NEF-QVF. Examples of conditional distributions  are the normal, binomial, beta, hypergeometric and geometric distributions, which are not all NEF-QVF.[1]
are the normal, binomial, beta, hypergeometric and geometric distributions, which are not all NEF-QVF.[1]
3. NEF-QVF have conjugate prior distributions on μ in the Pearson system of distributions (also called the Pearson distribution although the Pearson system of distributions is actually a family of distributions rather than a single distribution.) Examples of conjugate prior distributions of NEF-QVF distributions are the normal, gamma, reciprocal gamma, beta, F-, and t- distributions. Again, these conjugate priors are not all NEF-QVF.[1]
4. If 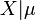 has an NEF-QVF distribution and μ has a conjugate prior distribution then the marginal distributions are well-known distributions.[1]
has an NEF-QVF distribution and μ has a conjugate prior distribution then the marginal distributions are well-known distributions.[1]
These properties together with the above notation can simplify calculations in mathematical statistics that would normally be done using complicated calculations and calculus.
References
- Morris C. (1982) Natural exponential families with quadratic variance functions: statistical theory. Dept of mathematics, Institute of Statistics, University of Texas, Austin.


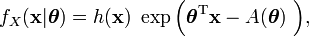




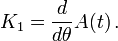
![\mu_1' = \kappa_1 = \mathrm{E}[X] = K'_X(0) = A'(\theta)\, .](../I/m/dfe9a448a73127868c544797419f1eb1.png)
![\mathrm{Var}[X] = \mu_2' = \kappa_2 + \kappa_1^2 \, ,](../I/m/8017b960075407266c4205392756bf33.png)
![\mathrm{Var}[X] = K''_X(0) = A''(\theta) \, .](../I/m/9bb690cb0038b68fdd1ce2fd87897e14.png)

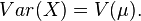
![X \sim NEF [\mu, V(\mu)] .](../I/m/bc4101d2707514ffdd905c345c8513c2.png)