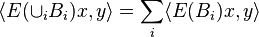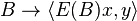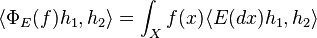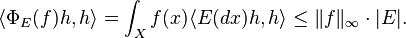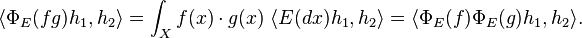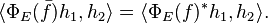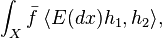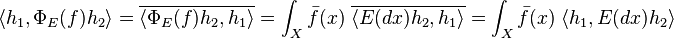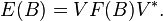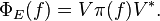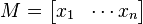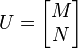Naimark's dilation theorem

In operator theory, Naimark's dilation theorem is a result that characterizes positive operator valued measures. It can be viewed as a consequence of Stinespring's dilation theorem.

Note

In the mathematical literature, one may also find other results that bear Naimark's name.

Some preliminary notions

Let X be a compact Hausdorff space, H be a Hilbert space, and L(H) the Banach space of bounded operators on H. A mapping E from the Borel σ-algebra on X to 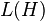$L(H)$ is called a operator-valued measure if it is weakly countably additive, that is, for any disjoint sequence of Borel sets 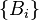$\{ B_i \}$ , we have

\langle E (\cup _i B_i) x, y \rangle = \sum_i \langle E (B_i) x, y \rangle

for all x and y. Some terminology for describing such measures are:

E is called regular if the scalar valued measure

B \rightarrow \langle E (B) x, y \rangle

is a regular Borel measure, meaning all compact sets have finite total variation and the measure of a set can be approximated by those of open sets.

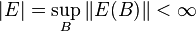E is called bounded if $|E| = \sup_B \|E(B) \| < \infty$ .

E is called positive if E(B) is a positive operator for all B.

E is called self-adjoint if E(B) is self-adjoint for all B.

E is called spectral if it is self-adjoint and 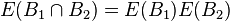$E (B_1 \cap B_2) = E(B_1) E(B_2)$ for all $B_1, B_2$ .

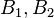We will assume throughout that E is regular.

Let C(X) denote the abelian C*-algebra of continuous functions on X. If E is regular and bounded, it induces a map 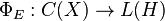$\Phi _E : C(X) \rightarrow L(H)$ in the obvious way:

\langle \Phi _E (f) h_1 , h_2 \rangle = \int _X f(x) \langle E(dx) h_1, h_2 \rangle

The boundedness of E implies, for all h of unit norm

\langle \Phi _E (f) h , h \rangle = \int _X f(x) \langle E(dx) h, h \rangle \leq \| f \|_\infty \cdot |E| .

This shows 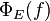$\; \Phi _E (f)$ is a bounded operator for all f, and 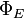$\Phi _E$ itself is a bounded linear map as well.

The properties of 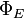$\Phi_E$ are directly related to those of E:

If E is positive, then 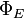$\Phi_E$ , viewed as a map between C*-algebras, is also positive.

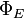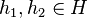$\Phi_E$ is a homomorphism if, by definition, for all continuous f on X and $h_1, h_2 \in H$ ,

\langle \Phi_E (fg) h_1, h_2 \rangle = \int _X f(x) \cdot g(x) \; \langle E(dx) h_1, h_2 \rangle = \langle \Phi_E (f) \Phi_E (g) h_1 , h_2 \rangle.

Take f and g to be indicator functions of Borel sets and we see that 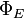$\Phi _E$ is a homomorphism if and only if E is spectral.

Similarly, to say 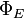$\Phi_E$ respects the * operation means

\langle \Phi_E ( {\bar f} ) h_1, h_2 \rangle = \langle \Phi_E (f) ^* h_1 , h_2 \rangle.

The LHS is

\int _X {\bar f} \; \langle E(dx) h_1, h_2 \rangle,

and the RHS is

\langle h_1, \Phi_E (f) h_2 \rangle = \overline{\langle \Phi_E(f) h_2, h_1 \rangle} = \int _X {\bar f}(x) \; \overline{\langle E(dx) h_2, h_1 \rangle} = \int _X {\bar f}(x) \; \langle h_1, E(dx) h_2 \rangle

So, taking f a sequence of continuous functions increasing to the indicator function of B, we get 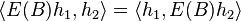$\langle E(B) h_1, h_2 \rangle = \langle h_1, E(B) h_2 \rangle$ , i.e. E(B) is self adjoint.

Combining the previous two facts gives the conclusion that 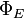$\Phi _E$ is a *-homomorphism if and only if E is spectral and self adjoint. (When E is spectral and self adjoint, E is said to be a projection-valued measure or PVM.)

Naimark's theorem

The theorem reads as follows: Let E be a positive L(H)-valued measure on X. There exists a Hilbert space K, a bounded operator 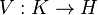$V: K \rightarrow H$ , and a self-adjoint, spectral L(K)-valued measure on X, F, such that

\; E(B) = V F(B) V^*.

Proof

We now sketch the proof. The argument passes E to the induced map 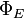$\Phi_E$ and uses Stinespring's dilation theorem. Since E is positive, so is 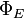$\Phi_E$ as a map between C*-algebras, as explained above. Furthermore, because the domain of 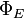$\Phi _E$ , C(X), is an abelian C*-algebra, we have that 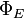$\Phi_E$ is completely positive. By Stinespring's result, there exists a Hilbert space K, a *-homomorphism 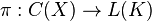$\pi : C(X) \rightarrow L(K)$ , and operator 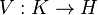$V: K \rightarrow H$ such that

\; \Phi_E(f) = V \pi (f) V^*.

Since π is a *-homomorphism, its corresponding operator-valued measure F is spectral and self adjoint. It is easily seen that F has the desired properties.

Finite-dimensional case

In the finite-dimensional case, there is a somewhat more explicit formulation.

Suppose now 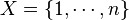$X = \{1, \cdots, n \}$ , therefore C(X) is the finite-dimensional algebra 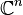$\mathbb{C}^n$ , and H has finite dimension m. A positive operator-valued measure E then assigns each i a positive semidefinite m X m matrix 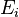$E_i$ . Naimark's theorem now says there is a projection valued measure on X whose restriction is E.

Of particular interest is the special case when 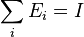$\; \sum _i E_i = I$ where I is the identity operator. (See the article on POVM for relevant applications.) This would mean the induced map 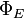$\Phi _E$ is unital. It can be assumed with no loss of generality that each 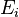$E_i$ is a rank-one projection onto some 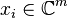$x_i \in \mathbb{C}^m$ . Under such assumptions, the case 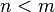$n < m$ is excluded and we must have either:

1) 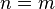$n = m$ and E is already a projection valued measure. (Because 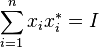$\sum _{i=1}^n x_i x_i^* = I$ if and only if 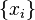$\{ x_i\}$ is an orthonormal basis.) ,or

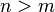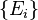2) $n > m$ and $\{ E_i \}$ does not consist of mutually orthogonal projections.

For the second possibility, the problem of finding a suitable PVM now becomes the following: By assumption, the non-square matrix

M = \begin{bmatrix} x_1 & \cdots x_n \end{bmatrix}

is an isometry, i.e. 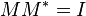$M M^* = I$ . If we can find a 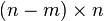$(n-m) \times n$ matrix N where

U = \begin{bmatrix} M \\ N \end{bmatrix}

is a n X n unitary matrix, the PVM whose elements are projections onto the column vectors of U will then have the desired properties. In principle, such a N can always be found.

References

V. Paulsen, Completely Bounded Maps and Operator Algebras, Cambridge University Press, 2003.