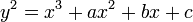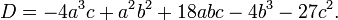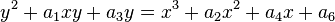Nagell–Lutz theorem

In mathematics, the Nagell–Lutz theorem is a result in the diophantine geometry of elliptic curves, which describes rational torsion points on elliptic curves over the integers.

Definition of the terms

Suppose that the equation

y^2 = x^3 + ax^2 + bx + c \

defines a non-singular cubic curve with integer coefficients a, b, c, and let D be the discriminant of the cubic polynomial on the right side:

D = -4a^3c + a^2b^2 + 18abc - 4b^3 - 27c^2.\

Statement of the theorem

If P = (x,y) is a rational point of finite order on C, for the elliptic curve group law, then:

1) x and y are integers
2) either y = 0, in which case P has order two, or else y divides D, which immediately implies that y² divides D.

Generalizations

The Nagell–Lutz theorem generalizes to arbitrary number fields and more general cubic equations.^[1] For curves over the rationals, the generalization says that, for a nonsingular cubic curve whose Weierstrass form

y^2 +a_1 x y + a_3 y = x^3 + a_2 x^2 + a_4 x + a_6 \

has integer coefficients, any rational point P=(x,y) of finite order must have integer coordinates, or else have order 2 and coordinates of the form x=m/4, y=n/8, for m and n integers.

History

The result is named for its two independent discoverers, the Norwegian Trygve Nagell (1895–1988) who published it in 1935, and Élisabeth Lutz (1937).

References

↑ See, for example, Theorem VIII.7.1 of Joseph H. Silverman (1986), "The arithmetic of elliptic curves", Springer, ISBN 0-387-96203-4.