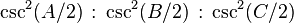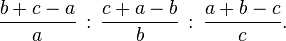Nagel point

In geometry, the Nagel point is a triangle center, one of the points associated with a given triangle whose definition does not depend on the placement or scale of the triangle. Given a triangle ABC, let TA, TB, and TC be the extouch points in which the A-excircle meets line BC, the B-excircle meets line CA, and C-excircle meets line AB, respectively. The lines ATA, BTB, CTC concur in the Nagel point N of triangle ABC. The Nagel point is named after Christian Heinrich von Nagel, a nineteenth-century German mathematician, who wrote about it in 1836.
Another construction of the point TA is to start at A and trace around triangle ABC half its perimeter, and similarly for TB and TC. Because of this construction, the Nagel point is sometimes also called the bisected perimeter point, and the segments ATA, BTB, CTC are called the triangle's splitters.
Relation to other triangle centers
The Nagel point is the isotomic conjugate of the Gergonne point. The Nagel point, the centroid, and the incenter are collinear on a line called the Nagel line. The incenter is the Nagel point of the medial triangle;[1][2] equivalently, the Nagel point is the incenter of the anticomplementary triangle.
Trilinear coordinates
The trilinear coordinates of the Nagel point are[3] as
or, equivalently, in terms of the side lengths a = |BC|, b = |CA|, and c = |AB|,
See also
References
- ↑ Anonymous (1896). "Geometry: 69-72". American Mathematical Monthly 3 (12): 329. JSTOR 2970994.
|chapter=ignored (help) - ↑ "Why is the Incenter the Nagel Point of the Medial Triangle?". Polymathematics.
- ↑ Gallatly, William (1913). The Modern Geometry of the Triangle (2nd ed.). London: Hodgson. pp. page 20.
- Baptist, Peter (1987). "Historische Anmerkungen zu Gergonne- und Nagel-Punkt". Sudhoffs Archiv für Geschichte der Medizin und der Naturwissenschaften 71 (2): 230–233. MR 0936136.
External links
- Nagel Point from Cut-the-knot
- Nagel Point, Clark Kimberling
- Weisstein, Eric W., "Nagel Point", MathWorld.
- Spieker Conic and generalization of Nagel line at Dynamic Geometry Sketches Generalizes Spieker circle and associated Nagel line.