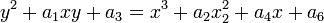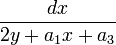Néron differential
In mathematics, a Néron differential, named after André Néron, is an almost canonical choice of 1-form on an elliptic curve or abelian variety defined over a local field or global field. The Néron differential behaves well on the Néron minimal models.
For an elliptic curve of the form
the Néron differential is
References
- Bosch, Siegfried; Lütkebohmert, Werner; Raynaud, Michel (1990), Néron models, Ergebnisse der Mathematik und ihrer Grenzgebiete (3) 21, Berlin, New York: Springer-Verlag, ISBN 978-3-540-50587-7, MR 1045822
- Néron, André (1964), "Modèles minimaux des variétes abèliennes sur les corps locaux et globaux", Publications Mathématiques de l'IHÉS 21: 5–128, doi:10.1007/BF02684271, MR 0179172