Multiple EM for Motif Elicitation
Multiple EM for Motif Elicitation or MEME is a tool for discovering motifs in a group of related DNA or protein sequences.[1]
A motif is a sequence pattern that occurs repeatedly in a group of related protein or DNA sequences. MEME represents motifs as position-dependent letter-probability matrices which describe the probability of each possible letter at each position in the pattern. Individual MEME motifs do not contain gaps. Patterns with variable-length gaps are split by MEME into two or more separate motifs.
MEME takes as input a group of DNA or protein sequences (the training set) and outputs as many motifs as requested. It uses statistical modeling techniques to automatically choose the best width, number of occurrences, and description for each motif.
MEME is the first of a collection of tools for analyzing motifs called the MEME suite.
Definition
What the MEME algorithms actually does can be understood from two different perspectives. From a biological point of view, MEME identifies and characterizes shared motifs in a set of unaligned sequences. From the computer science aspect, MEME finds a set of non-overlapping, approximately matching substrings given a starting set of strings.
Use
With MEME one can find similar biological functions and structures in different sequences. One has to take into account that the sequences variation can be significant and that the motifs are sometimes very small. It is also useful to take into account that the binding sites for proteins are very specific. This makes it easier to reduce wet-lab experiments (reduces costs and time). Indeed to better discover the motifs relevant from a biological point of view one has to carefully choose:
- The best width of motifs.
- The number of occurrences in each sequence.
- The composition of each motif.
Algorithm Components
The algorithm uses several types of well known functions:
- Expectation maximization (EM).
- EM based heuristic for choosing the EM starting point.
- Maximum likelihood ratio based (LRT-based). Heuristic for determining the best number of model-free parameters.
- Multi-start for searching over possible motif widths.
- Greedy search for finding multiple motifs.
However, one often doesn't know where the starting position is. Several possibilities exist:
- Exactly one motif per sequence.
- One or zero motif per sequence.
- Any number of motifs per sequence.
Example
In the following example, one has a weight matrix of 3 different sequences, without gaps.
| 1: | C G G G T A A G T |
| 2: | A A G G T A T G C |
| 3: | C A G G T G A G G |
Now one counts the number of nucleotides contained in all sequences:
| A: | 1 2 0 0 0 2 2 0 0 | 7 |
| C: | 2 0 0 0 0 0 0 0 1 | 3 |
| G: | 0 1 3 3 0 1 0 3 1 | 12 |
| T: | 0 0 0 0 3 0 1 0 1 | 5 |
Now one needs to sum up the total: 7+3+12+5 = 27; this gives us a "dividing factor" for each base, or the equivalent probability of each nucleotides.
| A: | 7/27 ≈ 0.26 |
| C: | 3/27 ≈ 0.11 |
| G: | 12/27 ≈ 0.44 |
| T: | 5/27 ≈ 0.19 |
Now one can "redo" the weight matrix (WM) by dividing it by the total number of sequences (in our case 3):
A: 0.33 0.66 0.00 0.00 0.00 0.66 0.66 0.00 0.00
C: 0.66 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.33
G: 0.00 0.33 1.00 1.00 0.00 0.33 0.00 1.00 0.33
T: 0.00 0.00 0.00 0.00 1.00 0.00 0.33 0.00 0.33
Next, one divides the entries of the WM at position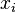 
with the probability of the base 
.
A: 1.29 2.57 0.00 0.00 0.00 2.57 2.57 0.00 0.00
C: 6.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 3.00
G: 0.00 0.75 2.25 2.25 0.00 0.75 0.00 2.25 0.75
T: 0.00 0.00 0.00 0.00 5.40 0.00 1.80 0.00 1.80
In general one would now multiply the probabilities. In our case one would have zero for every one. Due to this we define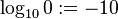 
and take the (base 10) logarithm:
| A : | 0.11 | 0.41 | -10 | -10 | -10 | 0.41 | 0.41 | -10 | -10 |
|---|---|---|---|---|---|---|---|---|---|
| C : | 0.78 | -10 | -10 | -10 | -10 | -10 | -10 | -10 | 0.48 |
| G : | -10 | -0.12 | 0.35 | 0.35 | -10 | -0.12 | -10 | 0.35 | -0.12 |
| T : | -10 | -10 | -10 | -10 | 0.73 | -10 | 0.26 | -10 | 0.26 |
This is our new weight matrix (WM). One is ready to use an example of a promoter sequence to determine its score. To do this, one has to add the numbers found at the position 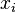of the logarithmic WM.
For instance, if one takes the AGGCTGATC promoter:
0.11 - 0.12 + 0.35 - 10 + 0.73 - 0.12 + 0.41 - 10 + 0.48 = -18.17
This is then divided by the number of entries (in our case 9) yielding a score of -2.02.
Shortcomings
The MEME algorithms has several drawbacks including:
- Allowance for gaps/substitutions/insertions not included.
- Ability to test significance often not included.
- Erased input data each time a new motif is discovered (the algorithm assumes the new motif is correct).
- Limitation to two component case.
- Time complexity is high, scaling O(n^2). A faster implementation of MEME, known as EXTREME, uses the online EM algorithm to significantly speed up motif discovery.[2]
- Very pessimistic about alignment (which might lead to missed signals).
See also
References
- ↑ Bailey TL, Williams N, Misleh C, Li WW (2006). "MEME: discovering and analyzing DNA and protein sequence motifs". Nucleic Acids Res 34 (Web Server issue): W369–373. doi:10.1093/nar/gkl198. PMC 1538909. PMID 16845028.
- ↑ Quang, Daniel; Xie, Xiaohui (February 2014). "EXTREME: an online EM algorithm for motif discovery". Bioinformatics 30 (12): 7. doi:10.1093/bioinformatics/btu093. PMC 4058924. Retrieved 19 August 2014.
External links
- The MEME Suite — Motif-based sequence analysis tools
- GPU Accelerated version of MEME
- EXTREME — An online EM implementation of the MEME model for fast motif discovery in large ChIP-Seq and DNase-Seq Footprinting data