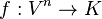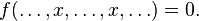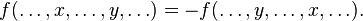Multilinear form
In mathematics, more specifically in abstract algebra and multilinear algebra, a multilinear form is a map of the type
where V is a vector space over the field K (and more generally, a module over a commutative ring), that is separately K-linear in each of its n arguments.[1]
For n = 2, i.e. only two variables, f is referred to as a bilinear form.
An important type of multilinear forms are alternating multilinear forms, which have the additional property of vanishing if supplied the same argument twice:
Special cases of these are determinant forms and differential forms.
When the characteristic is not 2, an alternating multilinear form is also antisymmetric, where the form changes sign under exchange of any pair of arguments:
The exceptional case of characteristic 2 does not share this property.