Multidimensional Chebyshev's inequality
In probability theory, the multidimensional Chebyshev's inequality is a generalization of Chebyshev's inequality, which puts a bound on the probability of the event that a random variable differs from its expected value by more than a specified amount.
Let X be an N-dimensional random vector with expected value ![\mu=\mathbb{E} \left[ X \right]](../I/m/49486c47f2280a304a0230eec6629c14.png) and covariance matrix
and covariance matrix
If 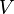 is a positive-definite matrix, for any real number
is a positive-definite matrix, for any real number 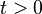 :
:
Proof
Since 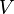 is positive-definite, so is
is positive-definite, so is 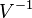 .
Define the random variable
.
Define the random variable
Since 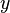 is positive, Markov's inequality holds:
is positive, Markov's inequality holds:
Finally,
![V=\mathbb{E} \left[ \left(X - \mu \right) \left( X - \mu \right)^T \right]. \,](../I/m/56f872eea22164b78ba0889da601fc93.png)
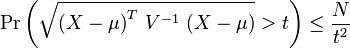
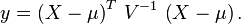
![\begin{array}{lll}\mathrm{Pr}\left( \sqrt{\left( X-\mu\right)^T \, V^{-1} \, \left( X-\mu\right) } > t\right) &= \mathrm{Pr}\left( \sqrt{y} > t\right)\\
&=\mathrm{Pr}\left( y > t^2 \right) \\
&\le \frac{\mathbb{E}[y]}{t^2} .\end{array}](../I/m/0c83278af5c190f0f9688911222448a6.png)
![\begin{array}{lll}\mathbb{E}[y] &= \mathbb{E}[\left( X-\mu\right)^T \, V^{-1} \, \left( X-\mu\right)]\\
&=\mathbb{E}[ \mathrm{trace} ( V^{-1} \, \left( X-\mu\right) \, \left( X-\mu\right)^T )]\\
&= \mathrm{trace} ( V^{-1} V ) = N \end{array}.](../I/m/c8fa157d862a779bdf6fdf35ee6a7d89.png)