Morse–Smale system
In dynamical systems theory, an area of applied mathematics, a Morse–Smale system is a smooth dynamical system whose non-wandering set consists of finitely many hyperbolic equilibrium points and hyperbolic periodic orbits and satisfying a transversality condition on the stable and unstable manifolds. Morse–Smale systems are structurally stable and form one of the simplest and best studied classes of smooth dynamical systems. They are named after Marston Morse, the creator of the Morse theory, and Stephen Smale, who emphasized their importance for smooth dynamics and algebraic topology.
For Morse–Smale systems on 2D-sphere all equilibrium points and periodical orbits are hyperbolic; there are no separatrice loops.
Gradient-like dynamical systems are particular case of Morse–Smale systems.
Theorem (Peixoto). The vector field on 2D manifold is structurally stable if and only if this field is Morse-Smale.
Examples
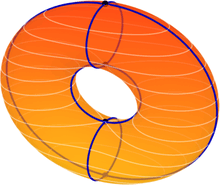

Any Morse function f on a compact Riemannian manifold M defines a gradient vector field. If one imposes the condition that the unstable and stable manifolds of the critical points intersect transversely, then the gradient vector field and the corresponding smooth flow form a Morse–Smale system. The finite set of critical points of f forms the non-wandering set, which consists entirely of fixed points.
References
- D. V. Anosov (2001), "Morse–Smale system", in Hazewinkel, Michiel, Encyclopedia of Mathematics, Springer, ISBN 978-1-55608-010-4
- Morse-Smale systems at Scholarpedia, curated by Dr. Michael Shub.