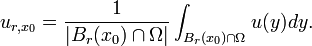Morrey–Campanato space
In mathematics, the Morrey–Campanato spaces (named after Charles B. Morrey, Jr. and Sergio Campanato) 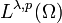 are Banach spaces which extend the notion of functions of bounded mean oscillation, describing situations where the oscillation of the function in a ball is proportional to some power of the radius other than the dimension. They are used in the theory of elliptic partial differential equations, since for certain values of
are Banach spaces which extend the notion of functions of bounded mean oscillation, describing situations where the oscillation of the function in a ball is proportional to some power of the radius other than the dimension. They are used in the theory of elliptic partial differential equations, since for certain values of  , elements of the space
, elements of the space 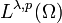 are Hölder continuous functions over the domain
are Hölder continuous functions over the domain 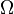 .
.
The seminorm of the Morrey spaces is given by
When 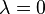 , the Morrey space is the same as the usual
, the Morrey space is the same as the usual 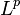 space. When
space. When 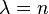 , the spatial dimension, the Morrey space is equivalent to
, the spatial dimension, the Morrey space is equivalent to 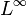 , due to the Lebesgue differentiation theorem. When
, due to the Lebesgue differentiation theorem. When 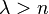 , the space contains only the 0 function.
, the space contains only the 0 function.
The seminorm of the Campanato space is given by
where
It is known that the Morrey spaces with 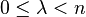 are equivalent to the Campanato spaces with the same value of
are equivalent to the Campanato spaces with the same value of  when
when 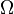 is a sufficiently regular domain, that is to say, when there is a constant A such that
is a sufficiently regular domain, that is to say, when there is a constant A such that 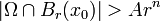 for every
for every 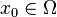 and
and 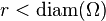 .
.
When 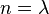 , the Campanato space is the space of functions of bounded mean oscillation. When
, the Campanato space is the space of functions of bounded mean oscillation. When 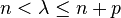 , the Campanato space is the space of Hölder continuous functions
, the Campanato space is the space of Hölder continuous functions 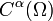 with
with 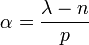 . For
. For 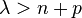 , the space contains only constant functions.
, the space contains only constant functions.
References
- Campanato, Sergio (1963), "Proprietà di hölderianità di alcune classi di funzioni", Ann. Scuola Norm. Sup. Pisa (3) 17: 175–188
- Giaquinta, Mariano (1983), Multiple integrals in the calculus of variations and nonlinear elliptic systems, Annals of Mathematics Studies 105, Princeton University Press, ISBN 978-0-691-08330-8
![\left[u\right]_{\lambda,p}^p = \sup_{0 < r< \operatorname{diam} (\Omega), x_0 \in \Omega} \frac{1}{r^\lambda} \int_{B_r(x_0) \cap \Omega} | u(y) |^p dy.](../I/m/ccedc5d618d7999515ef0f6c5a4c3571.png)
![\left[u\right]_{\lambda,p}^p = \sup_{0 < r< \operatorname{diam} (\Omega), x_0 \in \Omega} \frac{1}{r^\lambda} \int_{B_r(x_0) \cap \Omega} | u(y) - u_{r,x_0} |^p dy](../I/m/f0f18c51c772ea775a686fca8313931e.png)